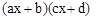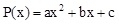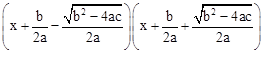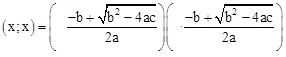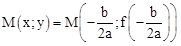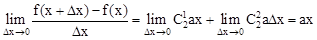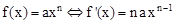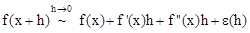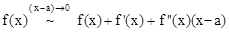Equations du second degré
Equation-du-2d-degre--application-numerique.pdf
_____________________________________________________________________________
Programme informatiques :
______________________________________________________________________________
Linguistique :
https-allemagne-equadeg-2.docx
Equadeg2--Cours-et-exercices-en-anglais.docx
____________________________________________________________________________________
____________________________________________________________________________________
Equation du second degré :
Une équation du second degré est issue d'un produit de deux facteurs du premier degré de la forme
Une équation du second degré est une expression algébrique homogène de la forme :
tel que
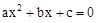
Ces solutions de cette équation ont pu être déterminées par sa forme canonique 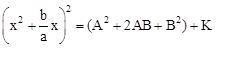
qui permet d’obtenir les facteurs canoniques
et les résultantes suivantes :
L’expression à l’intérieur d’une racine ne peut être que positive ou nul, il vient que cette expression littérale composés d’une différence est affectée d’un symbole grec Δ lu delta, appelé discriminant. Il vient que selon le signe de delta ( Δ ), nous possédons alors trois solution différentes :
A partir de l’équation du second degré, on peut construire une suite de points dans le repère orthonormé ( axes orthogonaux et munis d’un centre et d’une mesure). L’ensemble de ces points géométriquement ou en géométrie analytique, soit analytiquement, une forme curviligne ou figure curviligne appelé courbe. La courbe représentative de l’équation du second degré se nomme Parabole. Le point suivant est un point remarquable de la courbe
tel qu’il se situe sur la courbe dans le repère othonormé sur le sommet de la parabole qui peut être le maximum de la courbe, ou le minimum de la courbe par rapport au branche de la courbe, appelé extrêmum. A partir de l’identité remarquable, on peut construire un différentiel :
Cette expression est appelé différentiel de Newton à partir du XVIème siècle qui depuis s’appelle Polynome dérivé, représentant une fonction dérivé en un point tel que nos mathématiciens formulent la dérivé de l'équation du second degré par l'expression 2 ax , soit plus généralement :
Cette formule va permettre de construire l’équation :
Tel qu’en posant h = x-a, l’expression devient
Cette équation s'appèle Equation de la tangente tel que l'ensemble de ces droites forment une tangente à la courbe, impliquant qu'entre deux points très proche l'un de l'autre, les tangentes successive dessine la parabole.
A découvrir aussi
Inscrivez-vous au blog
Soyez prévenu par email des prochaines mises à jour
Rejoignez les 26 autres membres