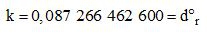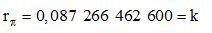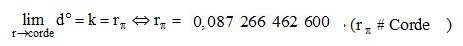Géométrie polygonale
__________________________________________________________________________________________________________________________________________________
16 Septembre 2015 : Aux Erudits :
Bon, là c'est la télé qui le dit, ce serait des truands très dangereux (Mathématique iles.net). Moi, je n'ai pas vérifier. Méthode inconnu dans les livres scolaire.Ceci si cette méthode est vrai, Très bonne approximation par rapport aux autres.
Quand à Wikipédia, c'est taylor déguisé. donc non.
15 Septembre 2015 :
Bon, ben voilà tu sais, mais épaississant le trait. et on le prend à l'extrême. Tes collègues ont raison (bien que ce soit la méthode), à la machine informatique, cela ne fonctionne pas. Et la recherche de la formule, prouve que l'angle est transcendantal, donc impossible à construire
05 Septembre 2015 : Discutions de bars - Trigonométrie, billard, nombre premier, billes pénalty, Cercle de Taylor, Tapisserie = papier millimétré, + notre problème, pourquoi la corde tend vers le rayon de l'arc, soit pourquoi la division de n arcs tend vers la corde.
De prime abord, on peut conclure que l'arc une divisé sachant qu'il fait 0,8662...., soit 0,87, diviser par n corde qui font 0,87 par la formule de Taylor Young, soit la corde tend vers l'arc, et donc la corde non multiple divisé par l'arc non multiple tend vers 1. Ce qui a comme conséquence que cos (alpha) / cos (alpha) tend vers 1. Pour quel raison : la projection orthogonal de la corde proche de l'arc au point p1 tend vers l'axe des abscisse à l'intérieur du cercle appelé axe des cosinus en ce point, Nommons le point p1 par C1. le centre du cercle étant O, alors la distance 0C1 à l'aide de la trigonométrie forme la valeur
R cos (alpha)=cos (alpha). Si on pose le point Cn représentant l'intersection entre le cercle et l'axe horizontale appelé axe des cosinus dans le cercle trigonométrique, forment un triangle CnMC1, ou M est le point d'intersection de la corde et du cercle. il vient que trigonométriquement la distance
restante est R - R cos (alpha) ou R(1- cos(alpha), ou 1 - cos(alpha) puisque R dans le cercle trigonométrique a pour unité 1, la corde représente l'hypothénuse du triangle CnMC1, appelons le côté et la distance opposé à l'axe des cosinus, le sinus (alpha) ou distance S, la distance de la corde étant l'hypothénuse, appelons la h.
Du théorème de pythagore, on a S²+( R - C)² = h²,
ou encore sin ² (alpha) + cos² (alpha) =1 ssi : sin² (alpha) = 1 - cos²(alpha) ou cos²(alpha) = 1 - sin² (alpha)
soit Sin ² (alpha) + (1 - cos( alpha))² = h²,
Soit h² = (1- cos²(alpha) + (1 - 2cos( alpha)+ cos²(alpha)
Soit h² = 2 ( cos(alpha)
Soit (h²/2) = cos²(alpha)
Afin d'abréger :
Par un autre moyen, on pourrait peut être trouvé unê formule hypothétique dans le style 1 - 2cos(alpha)sin(alpha)+ sin² (alpha) sans être sûr de moi, tel qu'à un moment donné on pourrait peut être obtenir la forme cos (alpha) / R - cos (alpha égalant un nombre infinitésimal soit dans les écritures moderne, on aurait sans aucune certituce cos (alpha) / R cos (alpha) tend vers 1 quand la corde h tend vers l'arc h' ou arc h' = arc CnM
Bon, je met ceci afin de m'en rappeler si un jour j'y retravaille, Formule d'addition, de duplication, de simpson, limites,
Si j'obtiens ce résultat, dès lors je met en évidence un lien entre la corde et l'arc, tel que cela rejoint aussi la formule d(OC1) / d (OM) = R(alpha) ou l alpha, tel que R ou l est la longeur de l'axe des cosinus il me semble sans aucune certitude.
_____________________________________________________
03 Décembre 2014 :
02 Décembre 2014 :

22 NOVEMBRE 2014 /
19 Novembre :
21H54 : Oui, bon, ben c'était stupide puisque :
La seule chose intéressante, est que la valeur n'est pas transcendantale.
15h39
15h16 : Bon, comme la musique, ça fait froid dans le dos. et comme les grands intellectuels ou génies. Des que je veux formuler son équation, la 40 degré est inconstructible. de 1 soit c'est un nombre transcendantale, soit c'est une approximation. Pour l'instant, celle que j'ai trouvé avec l'informatique, soit finalement la solution étatique, est en fait la formule de Taylor, qui elle est déjà une approximation en dessous quelque millième pour la plupart, et pour d'autre à 10^-9. Alors malgré les apparence, où j'ai réellement résolue la 40 degré depuis longtemps, soit avec pi, sur 100 mètre, la 40 degré devient constructible, puisque au millimètre 0,0872662 devient 8,262 mètre.
La valeur exacte est :
| 0,087266462600 |
Constante circulaire du degré régulier ( rayon du cercle = corde, ou rayon du cercle très peu différent de la corde, ou la limite de la corde = rayon )
J'aurais pu encore l'appeler rayon indice soit à partir de pi du degré régulier
Soit sans calcul analytique, mais littérairement, en mathématique on peut exprimer ce rayon de la manière suivante :
D'ailleurs à ce propos, la limite du rayon quand il tend vers la corde réel semblerait être la valeur 6,3742.10^-4 informatiquement
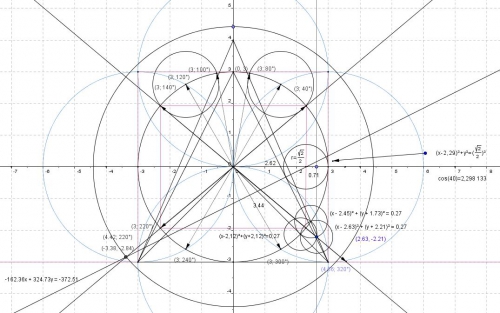
En informatique, on choisira la formule de Taylor, qui elle sur 3cm, avec un papier millimétré nous permet d'obtenir 2,298 cm sur 2,298 1 (2,298 133), et par extension 5 cm (3,830 222) voir 10 cm (7,860 444) ; 4cm (3, 064 177)
Sur 30 cm de longueur, on peut obtenir : 22, 981 cm qui peut faire office de valeur étalon.
2h ou 3h du math,
Bon, on constate que la 40 est essentiel à la construction du rapporteur, puisque
40-36 = 2
90-(40*2)=10 ; 40/2=20 ; 20/2 = 10 ; 10/2 =5
(36-30) / 2 = 3
La perpendiculaire à 40 amène 100 degré, et donc son équation, alors que le cercle, bien que ce soit l'intersection de deux cercles n'amènera une équation directe, mais on obtiendra une équation indirecte.
Bon je n'ai pas encore étudié la trisection, mais jusqu'à maintenant, dès la mise en équation, vérifié par le zoom, toutes mes méthodes pour construire la 40 degré, ont échoué.
Personnellement, sans connaitre la 40 degré, il ne reste plus que la 0,082662. On pourrait se dire que par rapport à Taylor, c'est ridicule. Et en fait par rapport au partage du cercle face à une construction inconstructible, c'est bel et bien la seule méthode, puisque toutes les intersection de cercles sont équidistant, sans passer par une construction approxmative. Certes c'est un nombre fini mais à 10^-9,
24H et quelques
18 Novembre
Euuuh, oui, ridicule, puisque calculer à partir de pi(), qui est en fait la valeur de Taylor. Ceci, en cas de perte de fichier, je vais l'installer dans la boite à fichier, parce que cela se trouve, à l'inverse de Will Hunting, je ne retrouverai peut être pas une telle valeur ( trans, approximation la meilleur possible, ect), soit la partie humaine.
le-degré-régulier-Avril-2012.xlsx
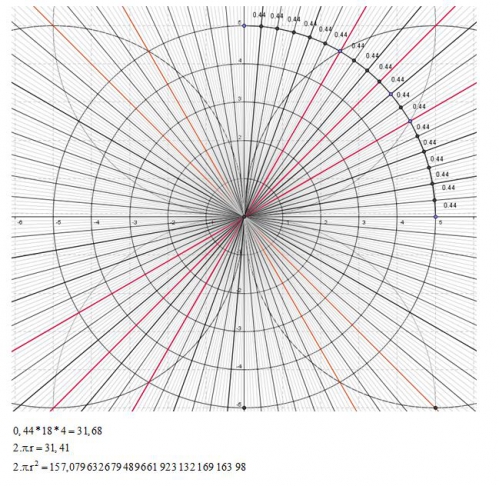
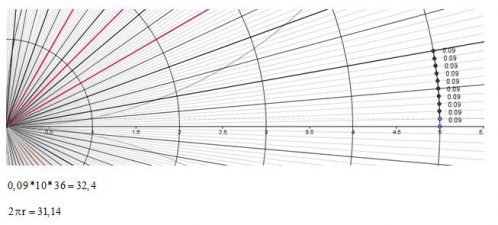
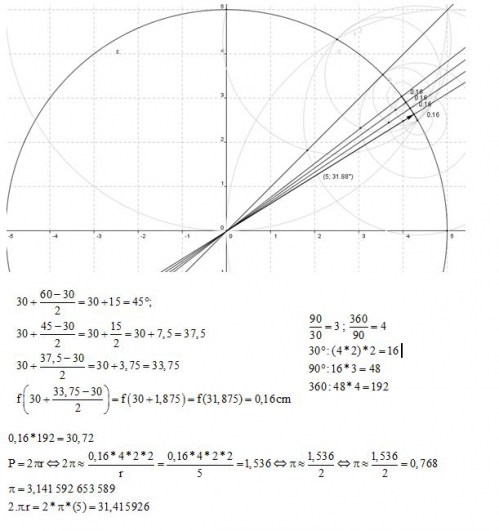
Euuuh rectificatif, là je suis sur 90 degré, d'où sur 360 degré :
| π | = | 192 × 0,16 | = | 3,072 |
| ──────── | ||||
| 10 |
Bon, voilà, parenthèse fermé.
___________________________________________________________________________________________________________________________________________________
14 NOVEMBRE 2014 :
__________________________________________________________________________________
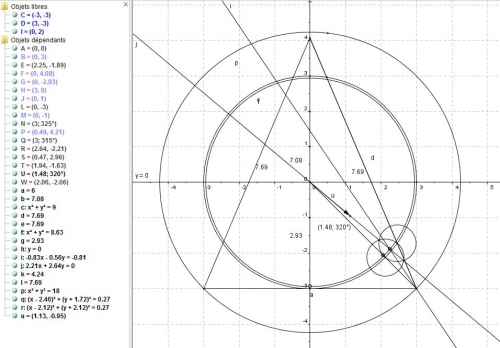
Enn--agone_par_le_triangle_3_cm__320_degr--__m--diatrice.html
_________________________________________________________________________________
__________________________________________________________________________________________
13 Novembre :
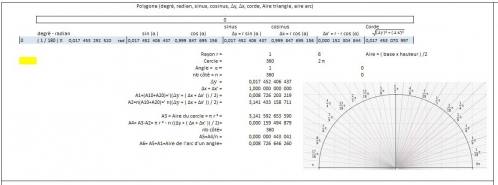
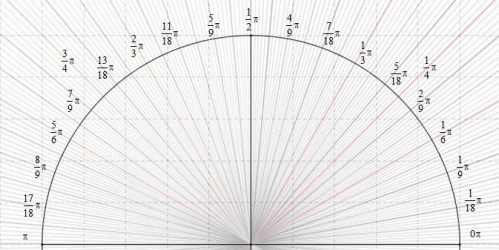
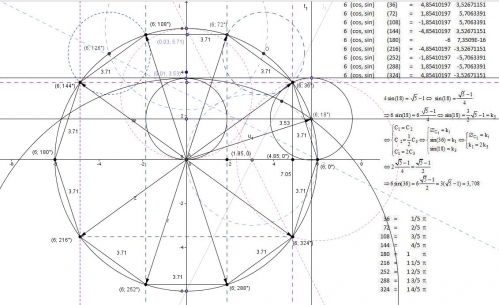
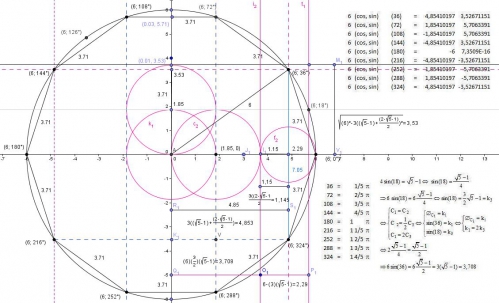
22 h 38 : le degré en radian
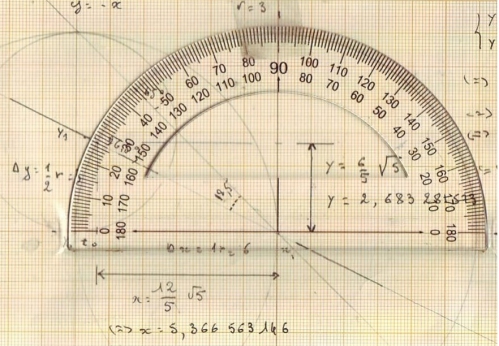
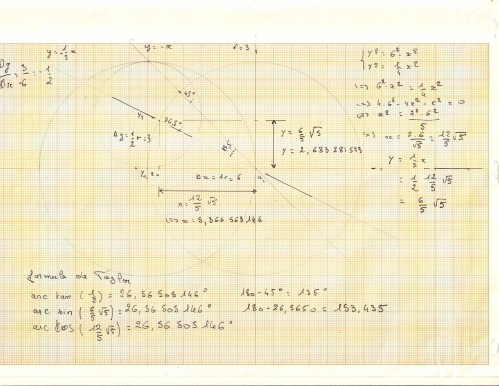
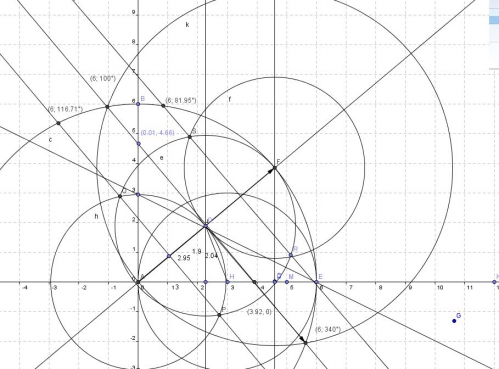
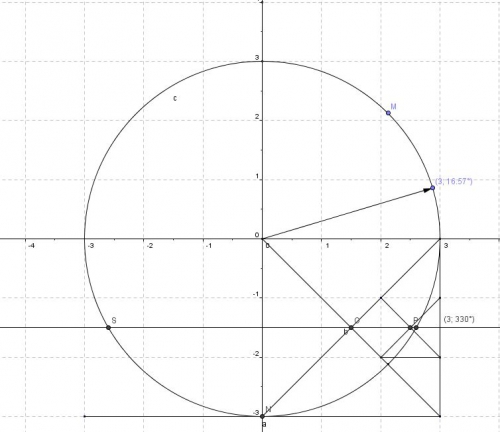
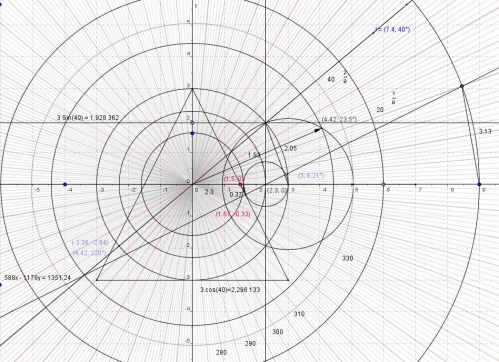
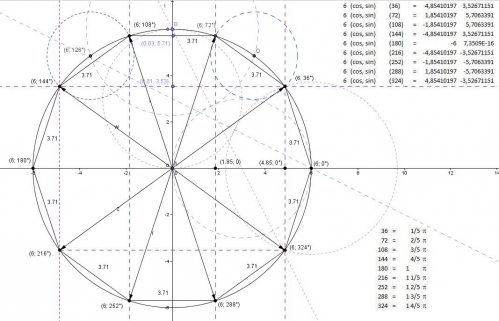
20h30 : ce n'est qu'une image, soit cette photo ne fonctionnera pas sur géogébra, mais c'est pour conserver les rapports en degré et radian :
3 cos(
Dans ce dessin, j'ai cru tenir enfin la loi, en réalité, nous avons dans (0,5)², soit racine carré de 2 sur 2, en fait 3- 3 cos (40) = 0,701 866. alros que racine carré ( 2 ) / 2 = 0,707 062 Soit seul les séries de Taylor permettent d'obtenir en informatique à 10^-3, la valeur 40 degré de manière surement très précise, de là à dire que cos (40) est une valeur exacte, elle est déjà une valeur approximative.
4 H 00 OU 5 H 00, La mauvaise nouvelle pour celui qui aime la construction, et la bonne nouvelle pour celui qui ne peut pas la construire :
3h 00 :
00 H 58
12 Novembre 2014 23h35
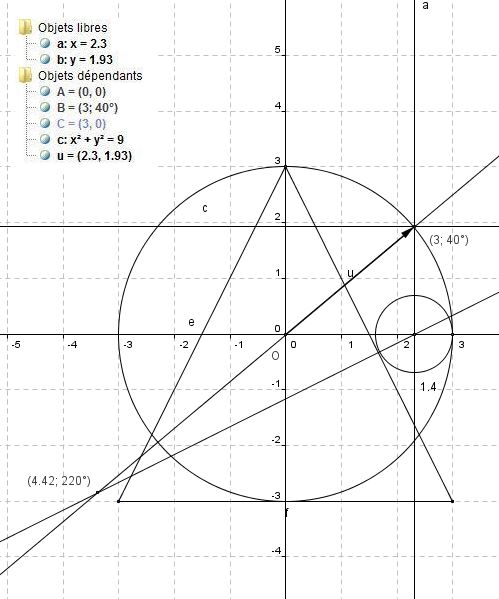
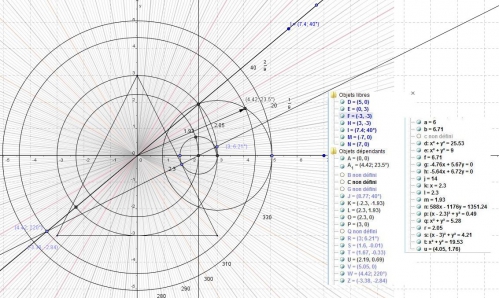
Ennéagone_détermination de l'angle de 40 degré_01.html
Le 12 Novembre : L'énnéagone
Bon, la méthode est simple, sur le rapporteur il tombe en plein centre ou à centième de gauche ou à droite du minimètre du rapporteur (Moi, il est en plein centre, mais sait on jamais. soit en informatique, j'ai une mesure entre 319,97 ..ou ..,98, ou 319,99. Voilà.
Bon, le degré, on divise le cercle en 360 partie, et il reste comme en physique 24 ou 25 jours.
Ceci dit depuis le début, on a trouvé une symétrie circulaire qui linéaire par le point de symétrie orthogonale à l'axe. Et c'est évident, l'énnéagone n'échape à cette règle :
Le problème, quand il faut faire le dessins à l'endroit, on ne peut pas trouver la symétrie, puisqu'elle n'est pas sur l'axe.
Bon, en zoomant, elle ne fonctionnerait pas à 10^-4. mais à 10^-2, c'est toujours le même point, donc cela reste une bonne aproximation
Autre fait étonnant :
Le 11 Novembre
Le 1 Novembre 2014
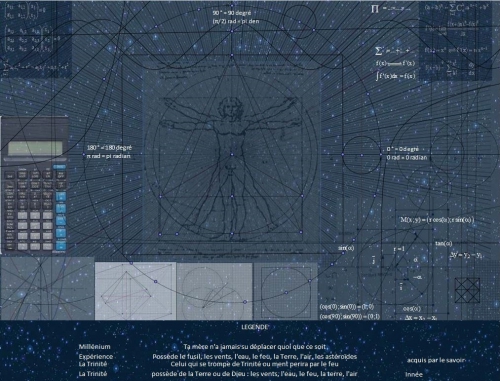
Bon, qu'est ce que nous apprend cette vidéo,
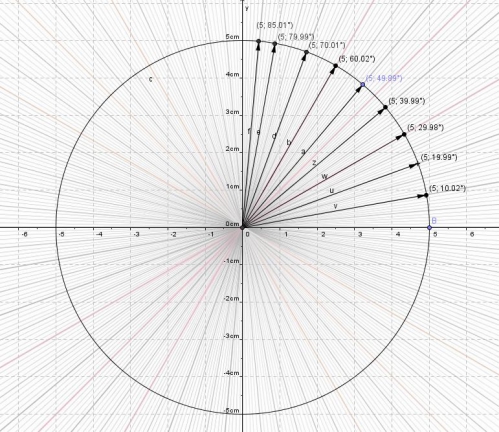
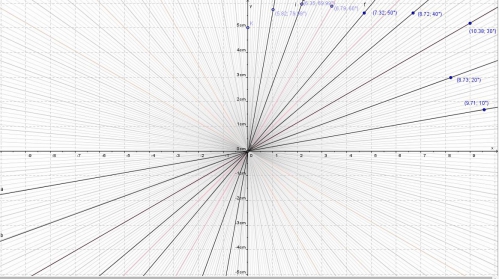
Un pied fait environ 5 degré,
le long pied fait environ 18 degré de loin, et de près à 15 degré, son symétrique est à environ 108°
Une main est 40, ou 42, et l'autre est à 24 ou 22, son symétrique semble etre est à 140-4, soit 144, et en réalité à 138
Bref, en plus d'être centralisé, de nous parler des nombres à traiter, elle nous parle aussi du maitre nombre 11 et 22, elle nous parle aussi des angles pair : 24,48,72,96,120,144
Plus sérieusement
108 divisé par (2,2,2,2...) =108 ; 54 ; 27 ; 13,5 ; 6,75 ect (visible sans rêgle.)
144 divisé par (2,2,2,2 ...) = 144, 72 , 36, 18, 9
24 multiplier par (2, 2,2,2,...) = 6, 12, ,24, 48, 72, 144
Bon, voilà, bien que ce soit un dessin fait par ordinateur, ce personnage représente la quintescence du 16 ième siècle tant dans le nombre de polygone que dans les suite de degré. Il représente la découverte de tous les degré, et des mesures métriques et trigonométriques. Il traite aussi des légende du siècle par la numéralogie
Le 30 Octobre 2014 :
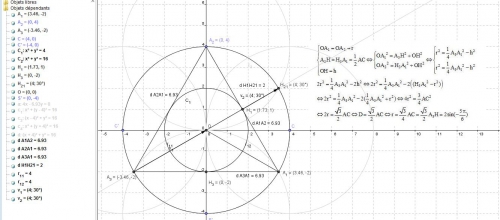
Bon, c'est une évidence même, je recherche à la fois l'angle au centre, et son mécanisme, je pourrais regarder dans un bouquin, mais en 1999, je l'ai trouvé à l'aide d'un exercice. Euuuh, il semblerait que ce serait a peu près le même, ou le même. Bon tout le monde a compris, en fait je cherche à la fois leurs aires, à la fois le partage du gateau, à la fois leurs dimension. Puisque je sais qu'il existe une formule générale :
Bon rectification
1/2 AiAi+1 + 1/4 AiAi+1=3/4 AiA+1
Le 29 Octobre 2014 :
Bon, ce n'est pas le même sujet, soit il parle littérairement de la corde, mais dans le fond, ce sont pour les même raisons, donc valide, même si nous n'y pensons pas :
Le 28 Octobre 2014 :
Bon, le nombre de Fabonnacci ne fonctionne que dans cercles particuliers, qui sont multiple de 24. Dans les déssins, cela aurait un lien avec le rapport d'un cercle de type circoncentrique, ou une succession de cercle à l'intérieur du cercle principale.
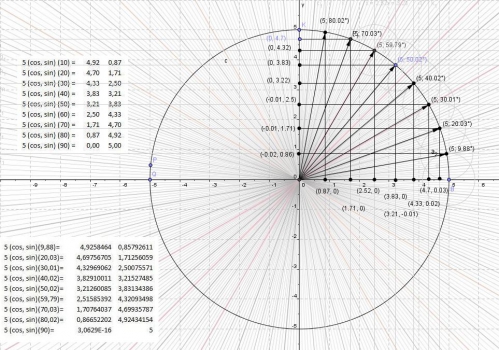
Toutefois, on constate bien que la trigonométrie par les séries limitées de Taylor Brook, permettent de calculer les coordonnées avec précision
L'inconvéniant est que cette méthode n'est la reproduction de la Nature, mais alpha - numérique.
Le 27 Octobre 2014
Bon, on arrête de rêver, c'est une réponse à la fois historique, a la fois métrique, mesure décimale, à la fois agencement naturelle puisque la nature n'a pas d'angle complémentaire, mais ne peut creer que des ronds, et des lignes, ou s'agencer comme l'araignée. Elle a aussi une valeur d'outil de contrôles des séries limitées de John Taylor, soit la calculatrice. Elle est aussi dans l'optique d'une fin du monde, avec risque d'outil informatique paralysér (U.V, Pluie, eau) dans le cas ou une partie de l'espèce humaine survie.
On rappelle qu'à l'aide du théorème de Thalès, on peut déterminer les autres valeurs numérique des cercles circoncentriques.
Bon, peut être que j'en ferais un exposé, avec vos méthodes et les notre ensuite, mais pour l'instant non.
26 Octobre 2014 ; 19 h 47
Bon, rien à voir avec eux, mes travaux en terme de progrès logique. Moi, ce qui me dérange, ce sont les décimales, quasi impossible à calculer, Et effectivement pouvoir déterminer les cordes, Voir si le degré est réellement une constante, Et c'est d'une évidence même, Etendre la formule. A l'aspect magique, en espérant que mes découvertes rejoignent les fameuses formules Corde, sinus, cosinus d'aujourd'hui avec un grand point d'intérrogation.
Bien, en réalité, dans géogébra, sans remettre en cause Géogébra, dans la circulation du vecteur, il s'avère que l'angle parfait, idéal, fonctionne par rapport à la circonférence, ce qui est stupide en soi, puisque pi est un nombre trascendantale, mais c'est un fait. il existe un lien entre le cercle et l'angle de manière idéale (soit, 0,000 cm et degré)
26 Octobre 2014
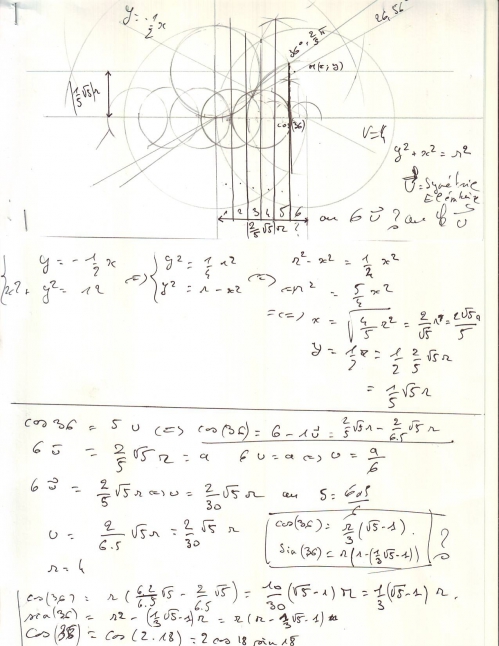
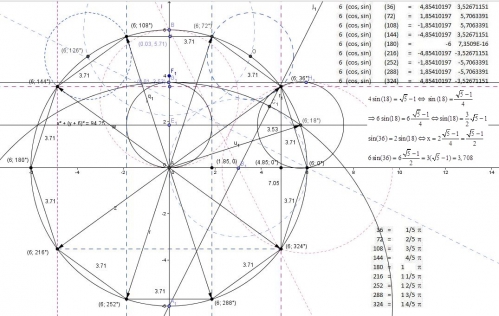
Bon, c'est évident, 2 sin (36) = sin (2.18)=2 sin (18) cos (18). Ceci, en effectuant les cercle, on voit bien que 2 sin (18) n'est le sin (36), mais la tangente du cercle de la corde. Soit 2 sin (18) donne la valeur de la corde dans le cas ou le rayon principal est r = 6 cm. ce n'est pas certain, que cela fonctionne dans les autres cercles circoncentrique. En même temps, avec Thales, Pytagore, on peut déterminer les autres valeurs, et peut être déterminer les cordes, avant d'émettre la formule de notre siècle.
Bon, là encore, on n'arrive peut être pas à me comprendre, mais que ce soit dans l'antiquité pour certaines figures, et surement au moyen âge, peut être plus vers le 16 ième ou jusqu'au 18 ième siècle, on essaie de conserver les décimales. Et effectivement, une valeur numérique avec décimal finie ou infinie, il nous est impossible de pouvoir calculer la valeur finale ( due au multiplication ou division). Donc la formule de la corde que nous utilisons, à l'époque, même s'il avait la formule littérale devait être quasiment impossible à appliquer. Soit il faut trouver par quel chemin ils sont passer aussi, c'est d'une évidence même.
26 Octobre 2014
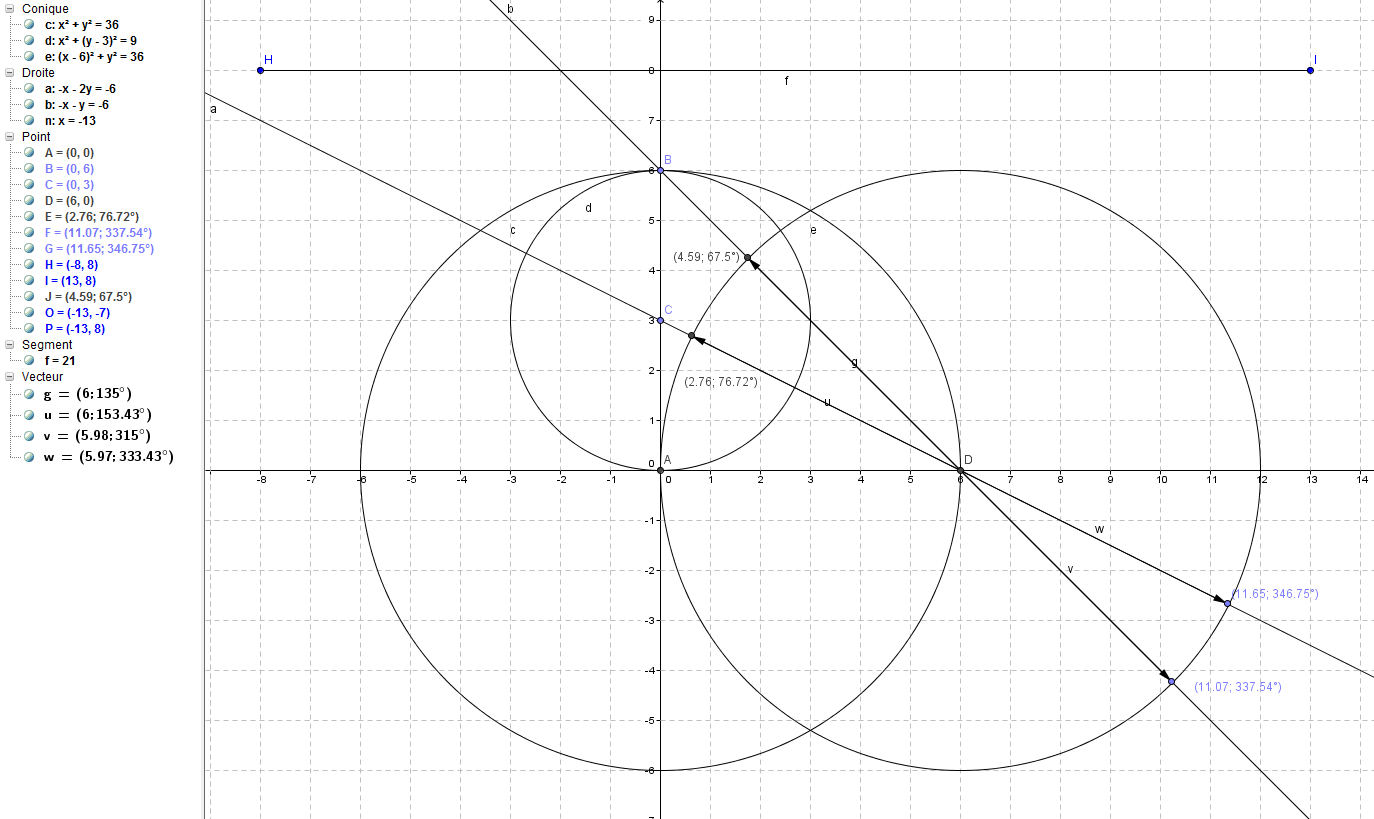
Alors Géogébra, soit moi, soit lui, relativement critiqué, non, c'est l'un des meilleurs au monde en terme de coordonées.
Et plus sérieusement à deux décimal près :
Mais la Raison principale est la suivante pour laquelle je la garde :
Bon, c'est une certitude intime malgré les contradiction qu'il est bel et bien en coordonnées rectangulaire et non pas circulaire. Apparemment il lui faudrait une accroche circulaire, ce qui complétement incongrue, dans la valeur des coordonnées rectangulaire. Dans les logiciel gratuit, c'est l'un des meilleurs au monde, bon, on a pas les décimales suivantes, donc on ignore si c'est 0,02, ou 0,00.
Enfin le degré est il réellement une constante, soit est ce que dans le fond ce ne serait pas géogébra qui ait raison ?
On sait depuis le début que le carré n'est pas inscriptible dans un cercle, on sait que ce sont les symétries qui permettent d'obtenir les valeurs identiques (soit symétrique). On sait qu'au papier, si l'on fait la sommes des angles succéssivement, nous avons le même problème. D'ou, on utilise les symétries.
Bon, voilà, on comprend rien en terme de valeur, soit comment les symétries en sachant ne fait pas 360 degré, réellement, mais 360,24 ou plus. que nos cercles succéssif sur la circonférence eux sont parfait, n'arrive pas à avoir les même valeur. Et pourtant c'est un fait. Et vis versa, par les symétries, en théories, nous ne pourrions pas obtenir des distances équidistantes des unes des autres
20 Octobre 2014
Bon, à la télévision, soit dans la météo, et quelques fois dans des émissions politiques, et parfois dans le journal télévisé, on a souvent dit :
On l'envie, c'est l'une des mains les plus sûre d'Europe, mais en arrière pensée en calcul numérique de Géogébra, c'est évident il s'accroche aux intersection, soit il y a un automatisme. Et en même temps, il est vrai, que si on est un peu trop loin de l'intersection à quelques dixième près, le point s'éloigne de l'intersection.
Bon, personnellement, par rapport aux axes, je suis à 0,01 cm du point d'accroche
Donc Géogébra en terme de distance est un calcul numérique et non pas une prise de mesure
Bon, voilà, je crois qu'on a tout dit cette fois
20 Octobre 2014
Bon le plan de travail à la Newtonniènne :
1) Trouver les angles
2) avant d'établir une formule littérale, intersection des cercles en valeurs numérique, soit 1, 2,3,5, 8,10,12,15,20,24 ... sytème d'équation d'équation d'intersection de cercle ( et programmation informatique).
3) Si cela colle, et seulement si cela colle, système d'équation trigonométrique
4) établir des formules algébrique, puis trigonométrique, puis exponentiel.
Soit comme les intersection de cercle, c'est un travail gigantesque.
20 Octobre 2014
Bon, la Télévision :
vrai, de par mon travail exhaustif, il y a peu de chance que le nombre d'or amène les 18 degré, ou les 24 degré. Toutefois, ce n'est pas un vrai travail, un vrai dossier, un vrai calcul littéral. Et vrai, sans les vrais origines, j'ai du mal à travailler un dossier. Est ce que c'est de la fainéantise, pfff, ces travaux vont peut être durer entre quelques semaines à quelques mois par expérience, et si cela se trouve, pour obtenir aucun résultat fiable. Donc, quand j'aurais le temps, quand j'aimerais, quand ça me passionnera. Pour l'instant, de par un travail très très suspicieux, aléatoire, exhaustif, mais qui me donne un ordre de grandeur viable puisqu'à chaque fois, j'ai toujours eu raison, cela ne me donne pas envie d'y travailler plus que ça. Et pis les valeurs scolaires ne m'interresse pas. Moi, ce que j'aime en math, c'est les vrais valeurs, et pas des valeurs virtuels
18 Octobre 2014
Réponse au clip : Pourquoi si tard ? :
De 1 le degré n'a jamais été ma priorité, ni pi, mais tout simplement les demandes Etatique et professoral. De 2, je ne sais vraiment pas si je suis la Trinité ou le Millénium, mais au cas où, je le fais. J'aurais attendu surement encore quelques années, soit d'abord la géométrie classique et vectorielle, avant le triangle d'or. Voilà ! Alors par rapport au Derby, De la à Laisser gagner Hollande sur l'incapacité, c'est niet. Il perdra, soit tout bas à droite d'une feuille excel.
12-11-2014
A découvrir aussi
Inscrivez-vous au blog
Soyez prévenu par email des prochaines mises à jour
Rejoignez les 26 autres membres