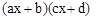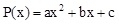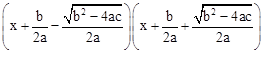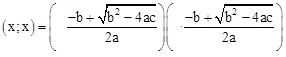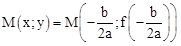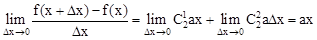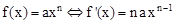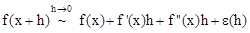Techniques des Mathématiques ( Niveau BEP, BAC ; Master, DESS)

E

Expression littérale : 

Expressions mathématiques composées de nombres (expressions numériques) et de lettres (expressions littérales) , de symboles exprimant la racine carrée, cubique, nième, le logarithme, l'exponentielle, les nombres complexes 

Expression numérique :

Expressions mathématiques composées uniquement de nombres,

Equation :

Egalité de deux expressions séparées par le terme "égal" à gauche et à droite des deux expressions

Equation homogène :

Expressions composées d'une expression littérale à gauche du terme avec un symbole "égal" et d'un membre nul à droite plus communément appelé zéro.

Equation du premier degré : 

l'équation du premier degré est une expression algébrique nul, soit muni d'une égalité tel que le membre de gauche est égal à zéro. cette équation est de la forme P(x) = ax + b ou y = ax + b tel que ax - y + b = 0. Quand y = 0, alors ax + b = 0. Dans un système cartésien qui est un plan muni de deux axes et d'une mesure métré ( un axe horizontal pouvant représenté la longueur apellé axe des abscisses, un axe verticale pouvant représenté la largeur ou la hauteur appelé axe des ordonnés) tel que ces deux axes sont orthogonaux, l'équation homogène de degré 1, donne un point qui a une coordonnée sur l'axe des abscisses par translation parallèle à l'axe des ordonnés, et sur l'axe des ordonnées par translation parallèle à l'axe des abscisses. L'ensemble de ces points forment une ligne rectiligne, soit horizontale, soit verticale, soit oblique, appelé droite. Le coefficient directeur a permet de donner la direction (horizontal, vertical, oblique) et le sens de la droite ( sens ascendant ou croissant, sens descendant ou décroissant).

Equation du second degré :

Une équation du second degré est issue d'un produit de deux facteurs du premier degré de la forme 

.

Une équation du second degré est une expression algébrique homogène de la forme :

.  

tel que

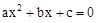
Ces solutions de cette équation ont pu être déterminées  par sa forme canonique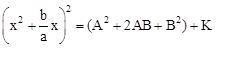

qui permet d’obtenir les facteurs canoniques 

  . 

et les résultantes suivantes :

 L’expression à l’intérieur d’une racine ne peut être que positive ou nul, il vient que cette expression littérale composés d’une différence est affectée d’un symbole grec Δ lu delta, appelé discriminant. Il vient que selon le signe de delta ( Δ ), nous possédons alors trois solution différentes :

A partir de l’équation du second degré, on peut construire une suite de points dans le repère orthonormé ( axes orthogonaux et munis d’un centre et d’une mesure). L’ensemble de ces points géométriquement ou en géométrie analytique, soit analytiquement, représente une figure ouforme curviligne appelé courbe. La courbe représentative de l’équation du second degré se nomme Parabole. Le point suivant est un point remarquable de la courbe

, 

tel qu’il se situe sur la courbe dans le repère othonormé sur le sommet de la parabole qui peut être le maximum de la courbe, ou le minimum de la courbe par rapport au branche de la courbe, appelé extrêmum. A partir de l’identité remarquable, on peut construire un différentiel :

Cette expression est  appelée différentielle de Newton à partir du XVIème siècle, qui depuis s’appelle Polynome(s) dérivé(s), représentant une fonction dérivé en un point tel que nos mathématiciens formulent la dérivé de l'équation du second degré par l'expression 2 ax , soit plus généralement : 

Cette formule va permettre de construire l’équation :

 Tel qu’en posant h = x-a, l’expression devient 

Cette équation s'appèle Equation de la tangente tel que l'ensemble de ces droites forment une tangente à la courbe, impliquant qu'entre deux points très proche l'un de l'autre, les tangentes successive dessine la parabole. 

F

Formule :

ensemble de termes algébriques formant une expression littérale générale

Formalisme :

ensemble de termes algébriques représentant la forme la plus condensée et la plus générale incluant ou non des sous formes masquées appelées expressions littérales colinéaires 

L

Ligne mathématique  (therme non scientique, non professorale, qu'utilisent les amateurs, et les professionnels en mathématique) : Expression littérale ou équations littérales, ou égalités littérales qui vont permettre la continuité de la résolution du problème théorique, soit une succéssion de developpement ligne par ligne, soit par une substitution, une permutation de membre à l'intérieur de l'expression littérale ou de l'égalité, une annulation ect.

______________________________________________________________________________________

Crée le 02 06 2012