GA) Trigonométrie
Retour sur la rubrique
Retour sur la rubrique précédente :
____________________________________________________________________________
Synthèse, Révision arithmétique, algébrique (3 pages), Formules trigonométriques, Equation de cercles, Intersections de cercle, dérivations et Intégrale trigonométrique, fonctions réciproques trigonométriques, dérivations, dérivations succéssives, suite numérique trigonométrique, PI, Matrice trigonométrique, le quaternion det (2 ; 2), Les polynôme de Tchebytchev
http://www.youtube.com/watch?v=PDxB-qnuCO4
____________________________________________________________________________
clip cinématographique : Oblivion (Tom Cruise) Bande annonce
( Alors bien que ce soit en 2D, effectivement il y a l'instersection des cercles et le quaternion, soit trigonométrie circulaire et matrice trigonométrique. Comme le film, c'est futuriste dans ma présentation)
Clip cinématophique (Oblivion, Version initiale des années 60-70)
_________________________________________________________________________________
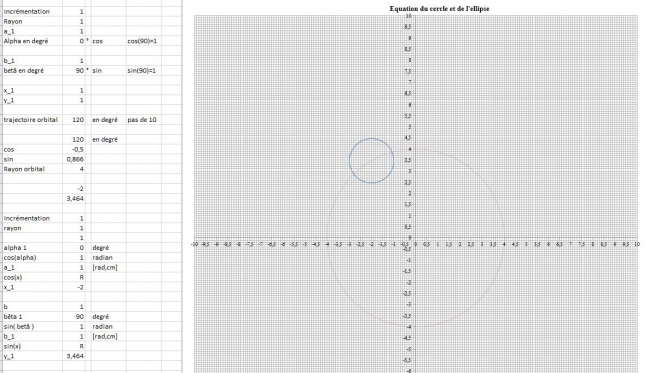
Formule exhaustive pour l'instant après un tel echec d'écriture mathématique puisqu'il y a encore à exprimer le passage du degré au radian avec pi
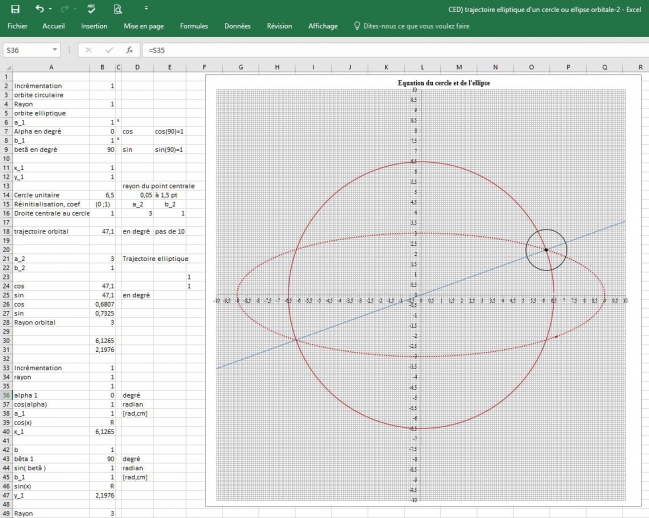
CCED--trajectoire-elliptique-d--un-cercle-ou-ellipse-orbitale (3)--26-12-2015.xlsx
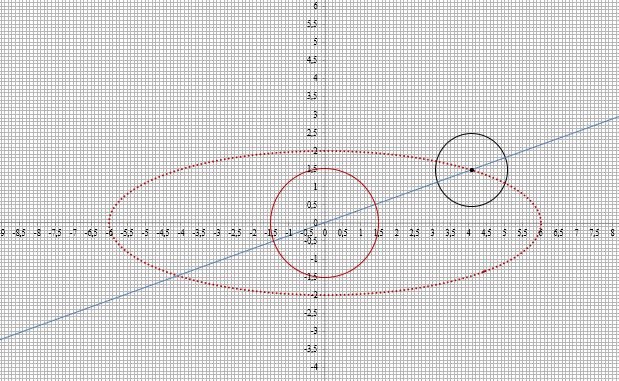
Bon, la version 3 a une toute petite différence, le point d'intersection de la droite, de l'ellipse et du cercle à 400 pt de zoom est bouché
bon, pas besoin de cos(alpha), cos (beta), soit X1 = a cos (x) ; Y1 = b cos (x)
________________________________________________________
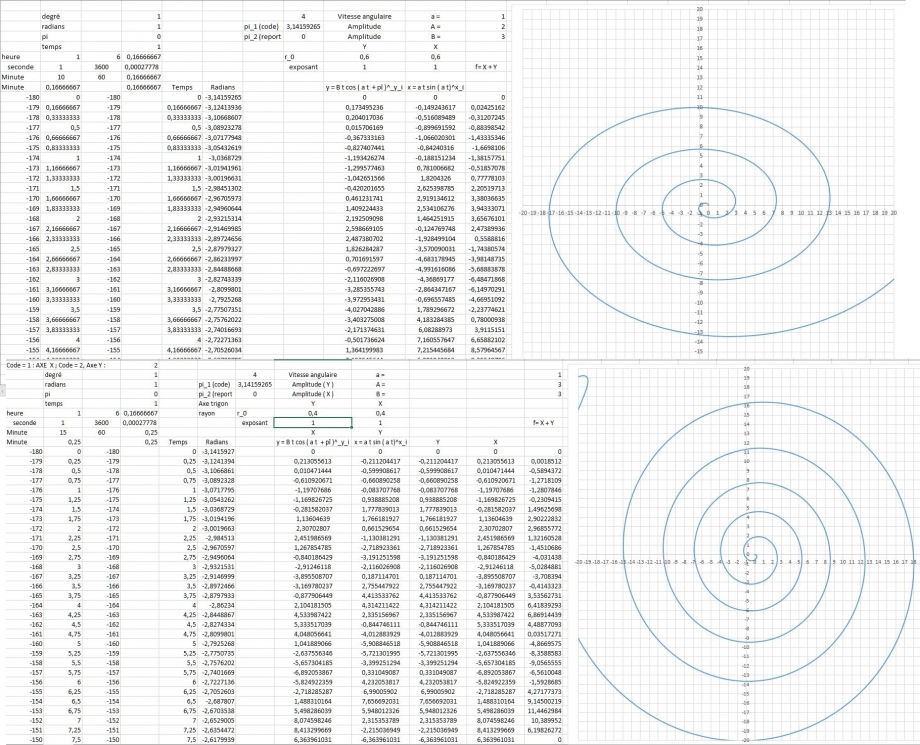
Cercle--ellipse--spirale (VO).xlsx
Cercles-lissés, intersection de cercle-Trigonométrie---06-01-2015.xlsx
Graphes-fonctions-polynomiales---trigonom--triques---23-01-2015---.xlsx
Comme dans la chanson, il n'est pas certain que ce soit la spirale officielle, et si ça l'est, et ben comme dans cette chanson :
________________________________________________________
Matrice trigonométriques (2011 : 11 ième place à la 19 ième place en 2013)
13 - Polynôme de Tchebytchev - 19-10-2016 - .pdf
http://www.youtube.com/watch?v=GhmRdQb0O7g
__________________________________________________________________________
Ancienne version :
Cercle--ellipse--spirale-02.xlsx
Cercle--ellipse--spirale-01.xlsx (Effet ellipsoïde)
___________________________________________________________________________
Forum : Forum mathématiques
Intersection de 3 cercle : Intersection de trois cercle
Bon, effectivement, je connaissais ces méthodes de calculs. Maintenant au niveau analytique, effectivement, il faut vérifier.
2013 : Vidéo sur Pi() : c'est arc cos (1-x).
3 D (Niveau Bac et Capès et master) :
Intersection de deux sphères :
____________________________________________________________________________
Equation trigonométrique anglais français (a cos (x) + b sin (x)
http://math.15873.pagesperso-orange.fr/IntCercl.html
Bon, pour être franc, je ne sais pas si ses solutions fonctionnent réellement dans les équations bicarrées qui sont résolvable, toutefois elle ressemble au notre.
____________________________________________________________________________
Le nombre PI :
a) Histoire des mathématiques : http://www.math93.com/pi.html
b) Tableau des nombres pi : http://www.gecif.net/articles/mathematiques/pi
Alors lui : Oui, archi oui :
c) Le nombre pi : http://www.pi314.net/ref/LE_NOMBRE_PI_TIPE_MPSI.pdf
4 Aout 2012 : (euuuh, Mor..., je n'ai pas encore ma paye, enfin je crois)
rayon 5 ; 15.7<x<15.6 environ: 15.65, 45,69, 15.70 Diamètre 10 soit 15.7/10 = 1.57
r= 4 ; 12.6<x<12.65 environ: 15,55 / ;60 / ;625, 15.70 Diamètre 8/8,1 soit 12.6/8.1 = 1.575
r= 3 ; 9.6<x<9.65 environ: 15,55 / ;60 / ;625, 15.70 Diamètre 9.5/ 3 soit 9.5/ 6,05 = 1.570 024
r=2 ; 6.4<x<6,5 environ 6.45 Diamètre 4/ 4,1 soit 6.4/ 4.1 = 1.573 170
Bon, tout le monde a compris qu'entre le débats, c'est un véritable fil tendu solide, et non pas un fil souple, puisque seul le papier découpé lui colle au chiffre à 0,000 1<x<0,000 001
D'autre part dans la bande annonce, que ce soit tout simplement une bande sur un cercle, oui, cela se pourrait. à quelque détail près : le 0,001<x<0,000 001, (et que cela reste entre nous, après avoir découpé le demi cercle, je n'ai absolument rien découpé ensuite pour obtenir une ligne linéaire, donc : )
_____________________________________________________________________________
31 Juillet 2012 : 9,5 <x<1.6 environ 9,5 / ,55 / ,60
Bon le rapport entre le diamètre du cercle et le demi cercle donne bien le rapport 3.14 / 2 = 1.57 à 1 cm près, refera l'expérience avec un fil fin souple. Pour l'instant :
rapport :
Pi = 3,141 592 6535897932384626433832795 / 2 = 1,570 796 3267948966192313216916398
Cercle de 5 cm de Rayon : 15.8 / 10.05 = 1,572 139 303
Cercle de 4 cm de Rayon : 12.8 / 8.20 = 1,573 170 731
Réflexion sur le nombre pi
Bien, malheureusement, je pense comme la plupart de ces articles, à une exeption près, que le rapport du diamètre du cercle et la longueur de longueur de l'arc est bel et bien une constante que l'on peut appeler pi. mais je pense qu'effectivementy il y a peu de probabilité que le rapport du diamètre et de la circonférence ou de la demi circonférence donne une valeur constante pi. mais cela, je ne l'ai jamais prouvé (dans le sens de compas, fil, ciseaux, dans un premier temps, et ensuite formulation dans différentes méthode). Je le pense sincèrement, hormis pour prendre une théorie déjà hasardeuse que l'on va démonter facilement et que les professionnel vont augmenter le niveau d'écriture pour la faire passer professionnelle et bac + 5 à 7.
D'autre part, je pense que tous le monde est d'accord sur ce sujet, je ne fabrique qu'un fascicule sur les formules fondamentale de niveau BEP à BAC, voire pour certaines notions utilisé en Bac, De deug, ou maîtrise, mais toujours pour revenir dans le cadre du BAC, mine de rien.
Maintenant est ce que pi a la valeur 3,141 592 653 589 793 238 462 643 383 279 5 après 3.141, toute la question est là. de toute façon, que ce soit en étude scolaire ou en étude mathématiquo-physique, il faut bien partir d'une base.
Franchement, je ne serais pas étonné que les demi cercles circoncentriques ait une valeur k(i).pi tel que k est soit une constance réellement de type a ou a/b, ou pire encore de type exponentielle en terme de courbe, c'est à dire soit croissante soit décroissante. maintenant la vraie problématique si k(i) soit à elle toute seule une véritable série soit continue, soit alternée, soit sans rapport constant (où là pseudo professionnel aurait une part trop belle à exploité).
Janvier 2011
Bon, 216 personnes, là, je pense franchement que c'est du footage de gueule... ou alors :
allez je vous la donne en scripturale, n'ayant pas démontrer totalement (série et rayon de convergence ? dans le sens prépondérance, ou importance capital):
pi = arc sin 1/2
arc sin ou sh (x) =( ( e^(1/2x) + e^(-1/2x) ) ÷ 2 = sigma de nombre impaire de la fonction exp (x)
exp(x) = sigma de i =1 à i=9 de x factoriel sur k factoriel ou inverse
____________________________________________________________________________
___________________________________________________________________________________
Crée le : 29 09 2009 - Modifié le 14/12/2015
Retour sur la catégorie Géométrie :
Retour sur la rubrique précédente :
Inscrivez-vous au blog
Soyez prévenu par email des prochaines mises à jour
Rejoignez les 26 autres membres