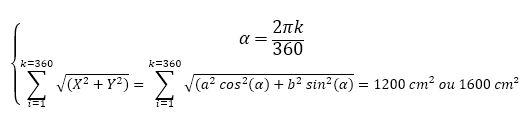Cercle, Ellipse, degré, trajectoire elliptique
31 Décembre 2015 :
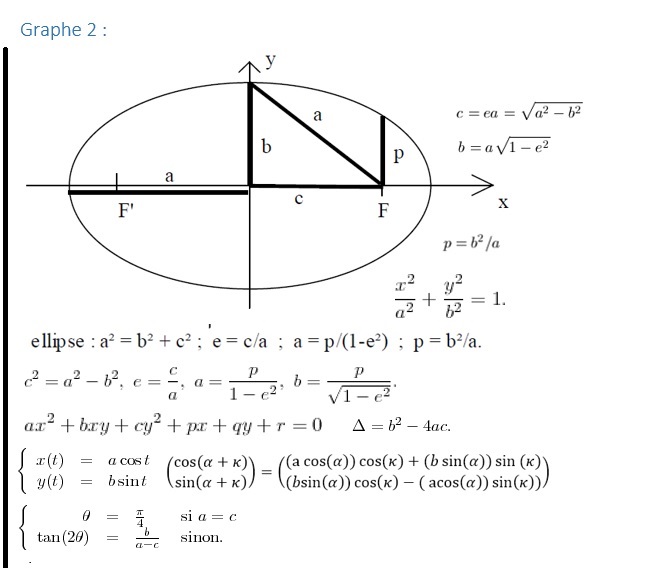
formulaire_sur_les_coniques.pdf
Bon, jusqu'à maintenant, homéomath, n'a jamais été vraiment génial, cette fois, il l'est :
http://homeomath2.imingo.net/ellipse.htm
http://www.askiitians.com/iit-jee-mathematics/coordinate-geometry/preparation-tips.html
___________________________________________
Bien Bernard Caseneuve, de tout ce que je lis, ce qui me semble le plus probable en terme d'ellipse à la fois constructible, à la fois très proche dans l'espace et sur terre ( De math curve) :
Quand aux russes et aux suisses, ils ont probablement raisons (soit de très proche de la réalité à très très proche) :
___________________________________________
Mise en équation :
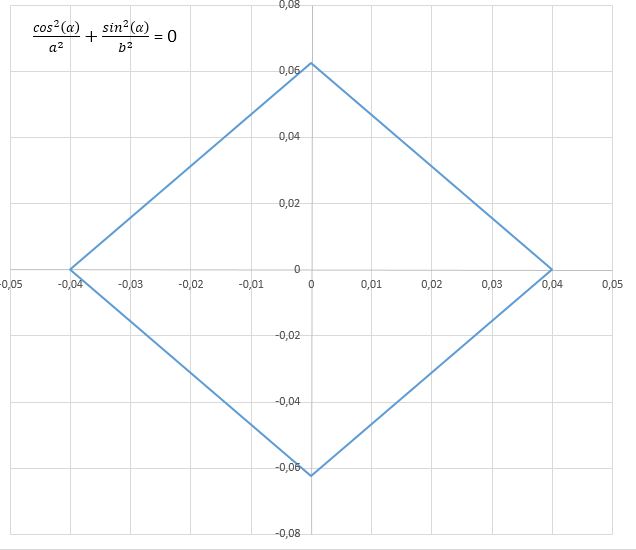
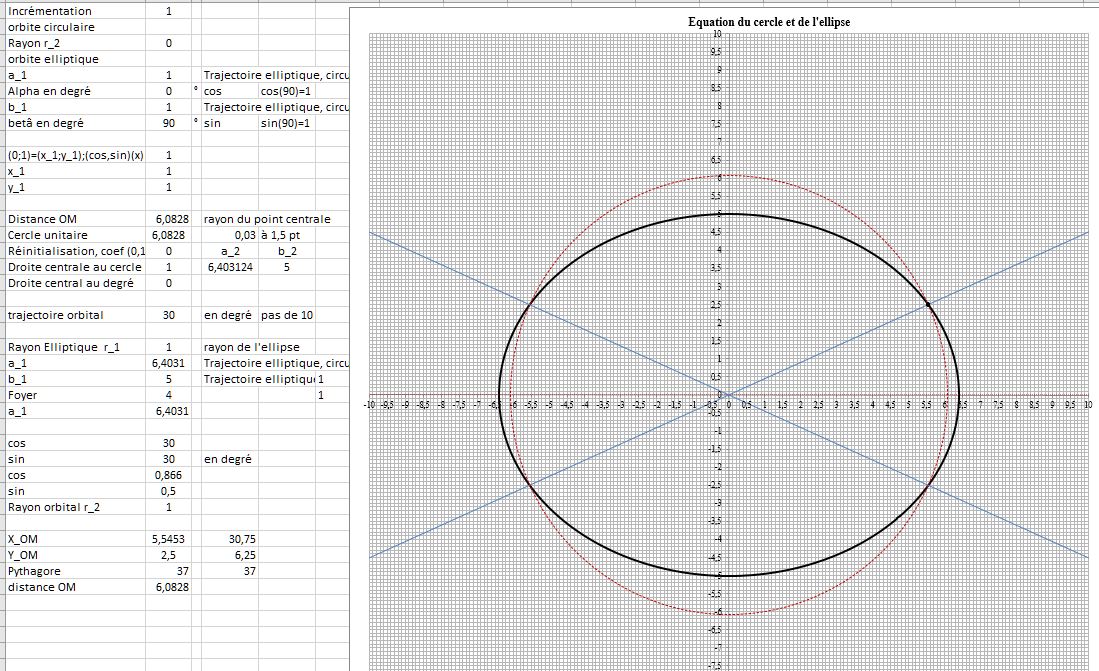
13/02-2016 : Equation trigonométrique et carthésienne de l'ellipse :
12-02-2016 : Au stylo, Recherche de l'équation d'aire de l'ellipse (qui l'Intégrale de Lesbesgue et de Rieman)
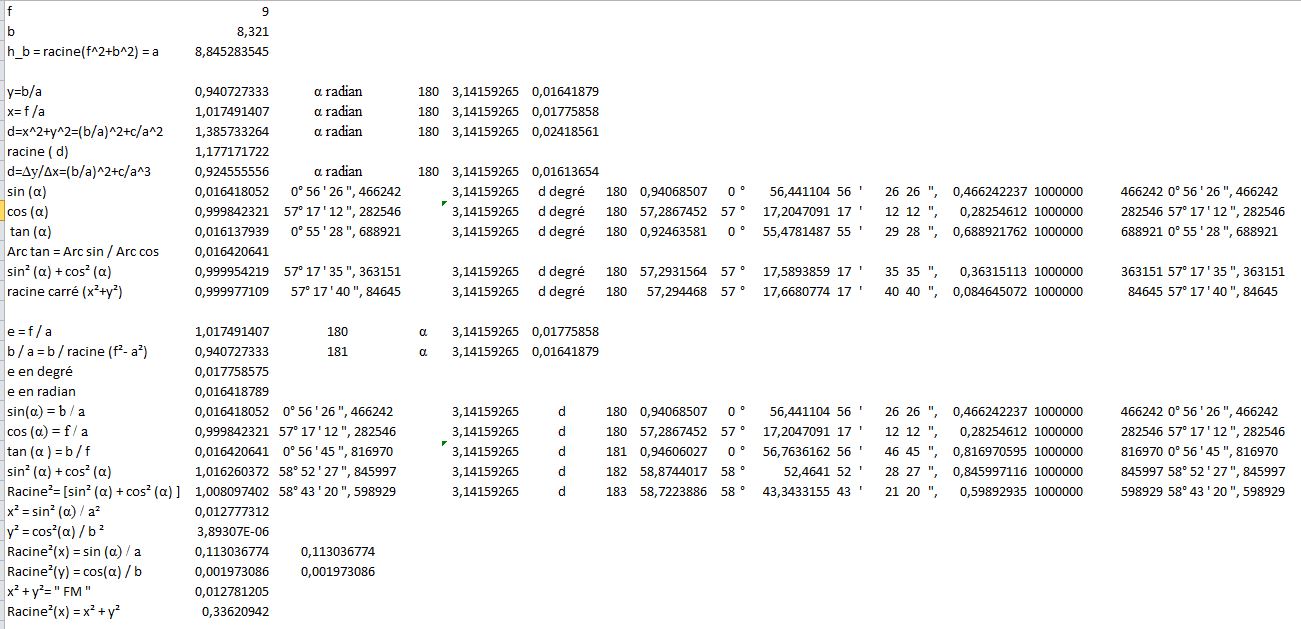
Bon la problématique selon le type d'élipse, est que la sommes des segment partant de son centre jusqu'à la circonférence est de 160 cm² ou 1270 cm², sachant que l'ellipse a pour (Foyer, axe mineur, axe majeur ) = ( 3 ; 4 ; 5 ) . et donc l'aire du rectangle estr de (3.2).(5.2)=60 cm² maximum. l'aire de l'ellipse selon le théorème de Pythagore est :
Et puisque l'aire de rectangle qui l'entoure est de 60 cm², cette méthode pour la première fois, n'est pas bonne
Rappelons que cette formule est la diagonale d'un carré, et donc la fonction affine dans l'intervalle I = [ 1 ; 360 ]
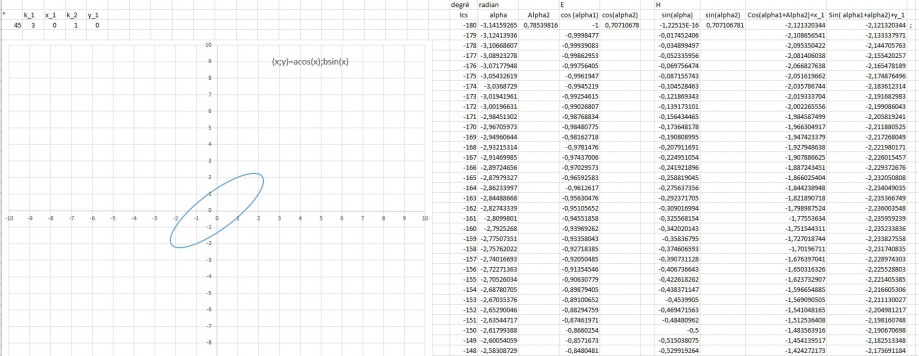
Depuis le début, dans le tracé, [ a cos (x) ; b sin (x) ] ne donne que le point pas la distance sur l'axe des abscisse, et l'axe des ordonnées, ce qui est incongru.
et pourtant un fait :
puisque dans le cercle, j'ai calculer de la même manière, et l'aire a donné 360 cm²
Equation-de-l--ellipse-14-02-2016.pdf
16-01-2016 / Equartion carthésienne de l'ellipse - FM, Math World
12-01-2016 ;: Equation carthésienne de l'ellipse, recherche de la symétrie
07-01-2016 : Equation paramétrée, courbe, Géogébra, rotation des angles dans l'ellipse
02-01-2015 : Graphe, Ellipse à axe symétrique oblique, définition bifocale de homéomath
01-01-2016 :Graphe, définition bifocale
14h00 : 20-12-2015
11-01-2016 : Développement d'équation carthésienne sans succès
_________________________________________________________________________
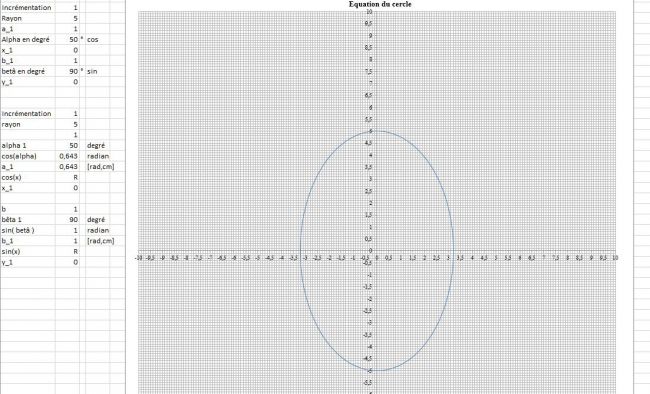
Graphe :
Enfin, par rapport à la Turquie : ce que je et nous avons ou pouvons calculer réellement pour l'instant malgré toutes les équations données :
12-02-2016 :
16-01-2016 :
Soit comme LBEI youtube, Ca, ce sont les fait réels
13-01-2016 /
Bien, par rapport à l'avalanche de la haute savoie (alpes) et autre commentaire : euuuuh :
ou :
d'autre part, de math world, je sais que :
OU .:
Recherchons la symétrie hypothétique :
Bon de même dans l'expression
a x^2 + 2 ab xy + y^2 + k x + k'y = 0
dans les coordonnées vectoriel, du produit scalaire i j = 0 => 2 ab x y i.j = 0 <=> 2 ab xy = 0 Ce qui reste à prouver en algèbre et en analyse
Maintenant Lyon ou Paris, hein, vous me foutez la paix les élèves, ce que je recherche, c'est la symétrie, le rapport proportionnel entre OA et OB qu amènera e, et aussi bien comme les professionnel de la télévision l'ont dit le tracé sur le papier et sur la machine, OK !
Bon voilà, c'est ce que je recherche.
12-01-2016 :
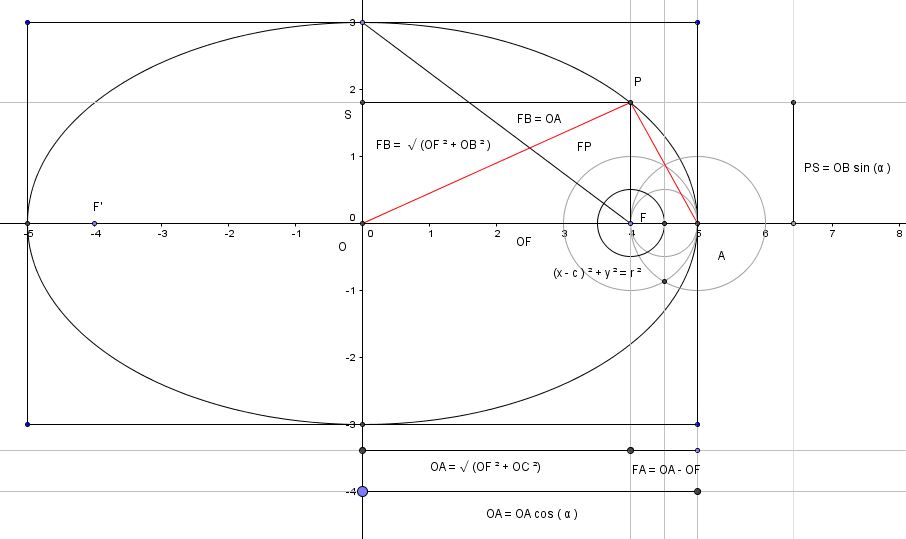
Sinon par rapport à x-c qui permet de construire les axes de l'ellipse au minimum :
Bon, c'est évident que cela dépend de OB, soit si c'est nombre non entier, peut être auront nous pas la même symétrie, ou aucune symétrie par rapport à OA. Mais dans N, c'est une certitude. il existe un rapport entre OA et OB, tel que ce rapport est une constante qui est liée à ( x - c ) ² + y² = r ²
Bon voilà, dans l'ensemble des nombres réels, lorsque OA et OB, ne sont pas proportionnel, il vient que je dois utiliser les deux axes de symétrie qui m'amène l'axe de symétrie centrale du O ( 0, 0). Mais ça, c'est logique (et stupide comme raisonnement). Donc l'ellipse dans N subit une loi rationnelle ( ou proportionnelle), tandis que dans R, n'a pas une loi rationnelle ou proportionnelle.
___________________________________________________________________________
20H29
12H30
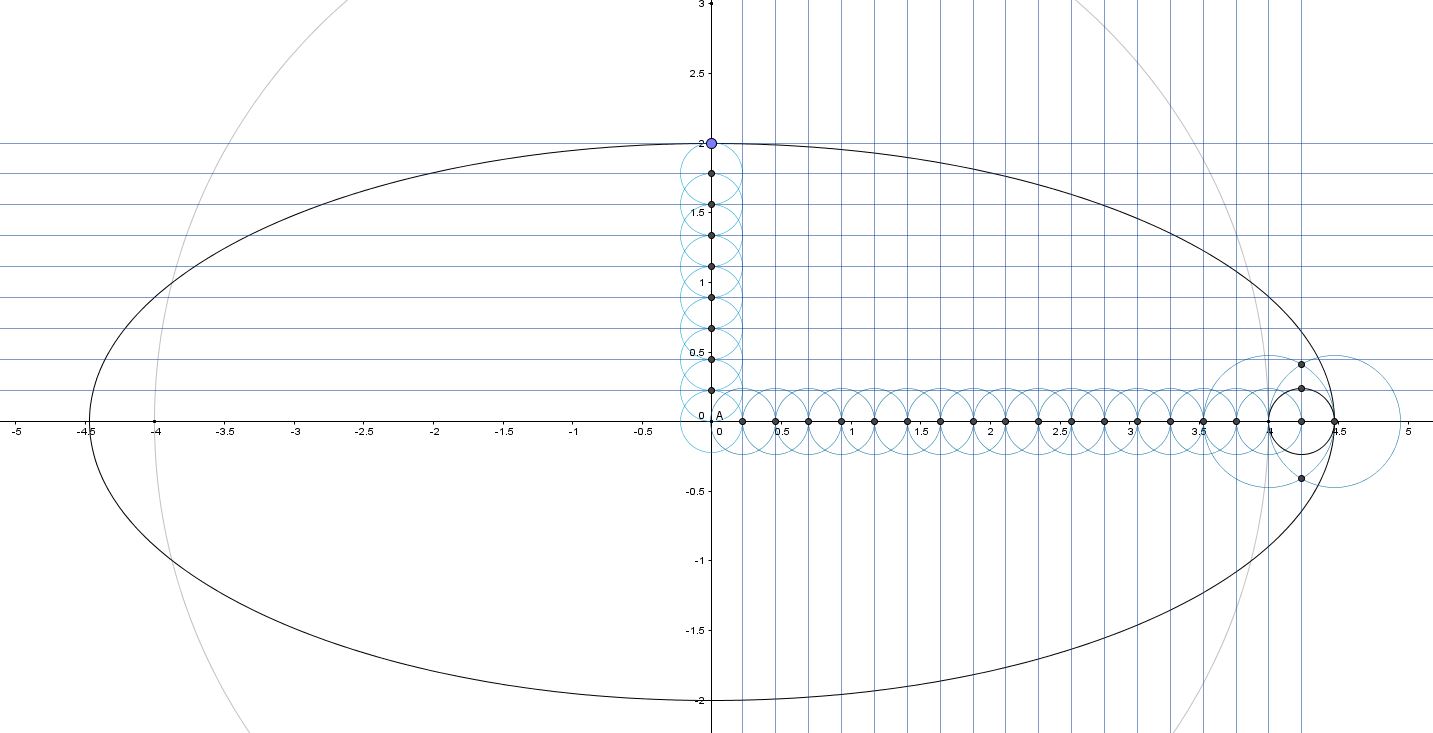
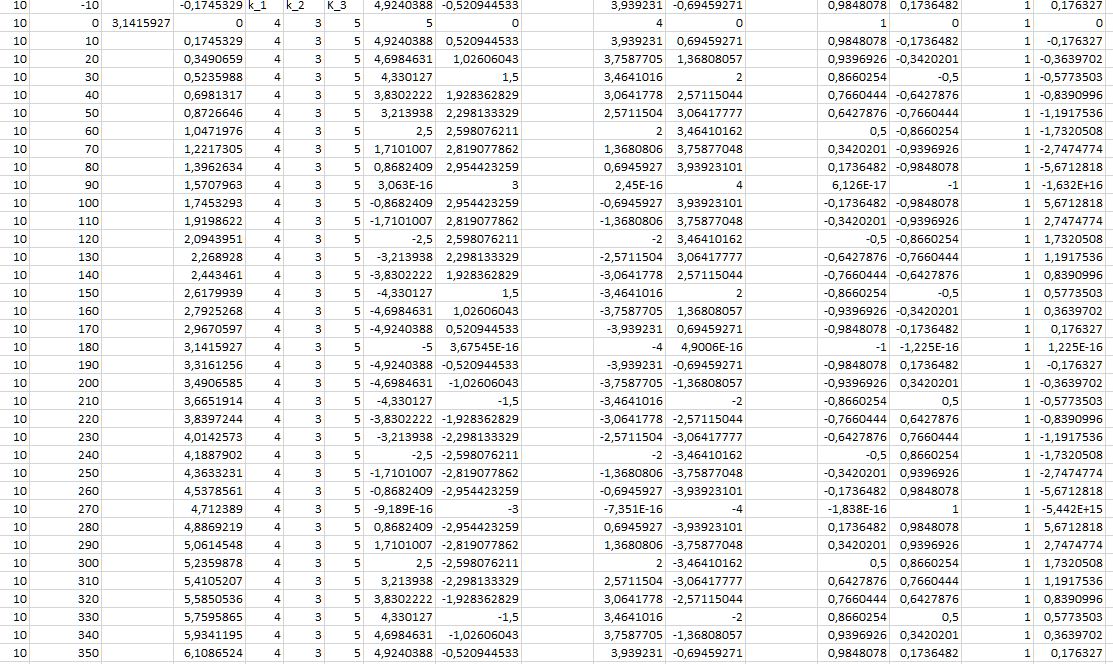
a cos (x), b sin (x) ; programme du 23 12 2016 - Horizontal, vertical
Bon en réalité : a cos (x1+x_2) ; b sin (x_1+x_2) ; Horizontal, Vertical, Oblique
09 01 2016 /
08-01-2016 /
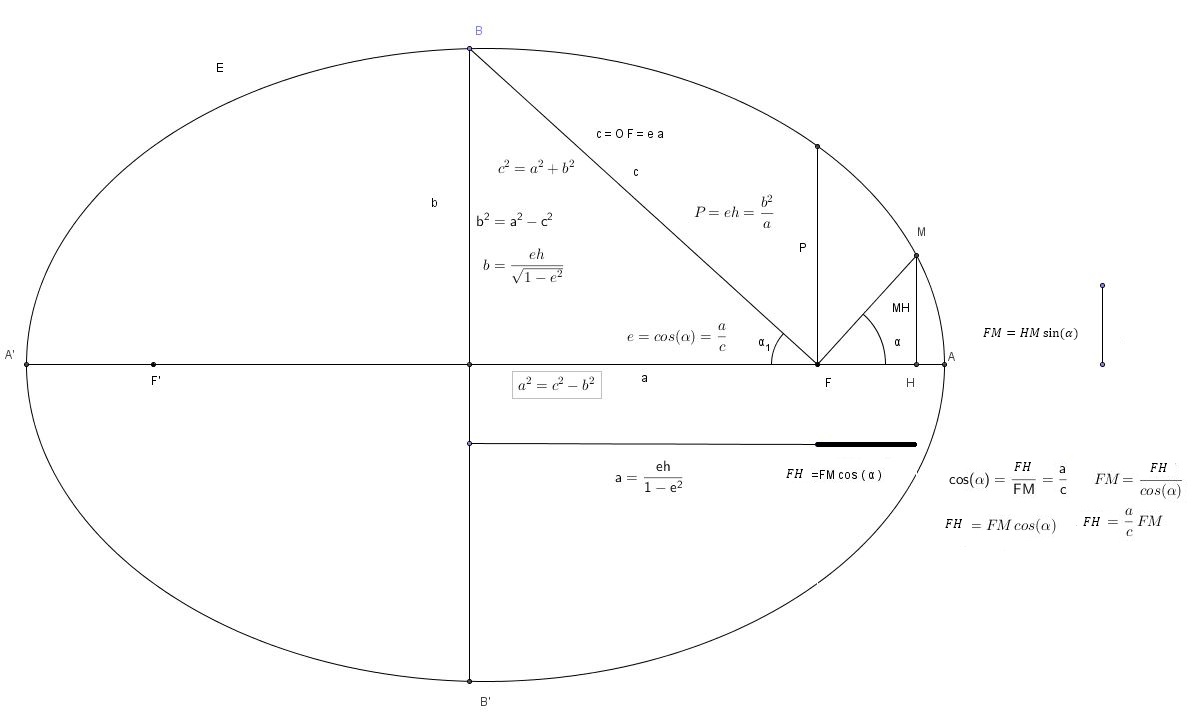
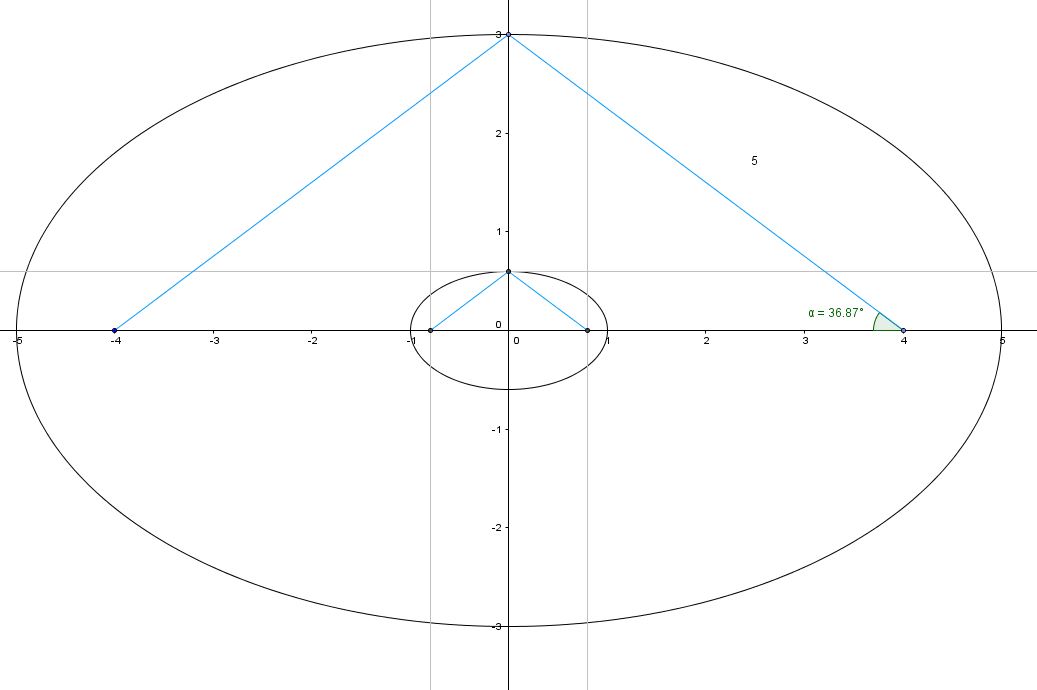
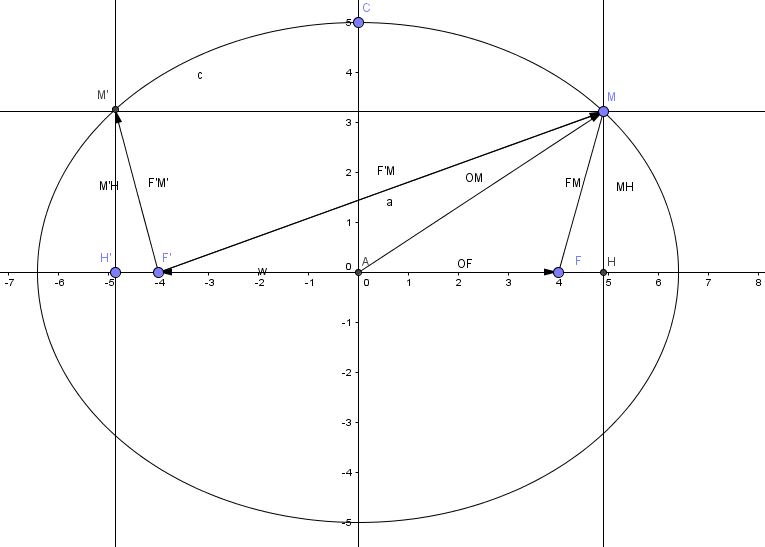
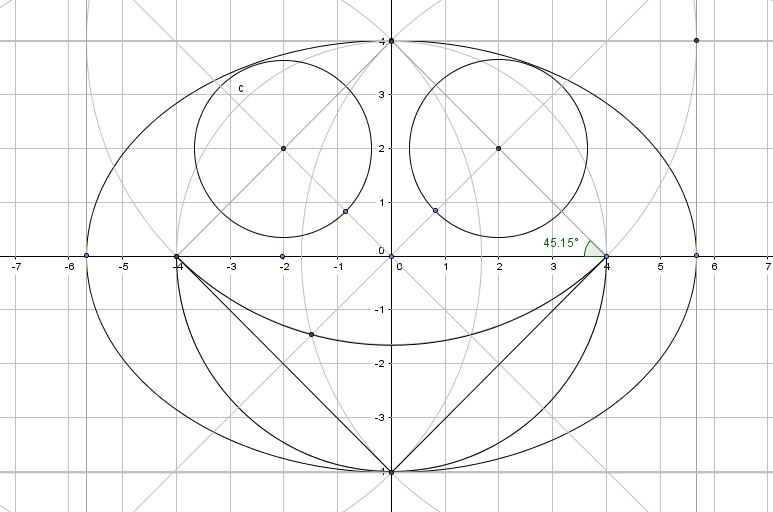
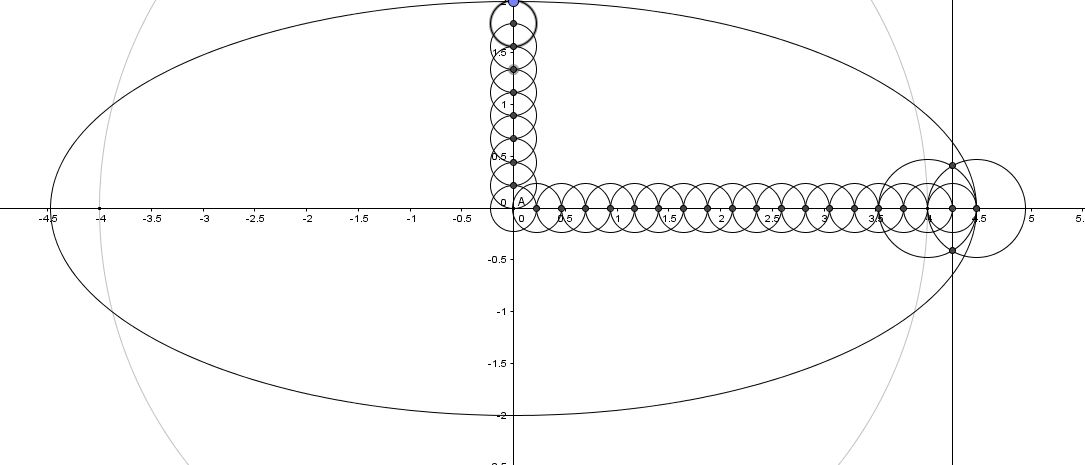
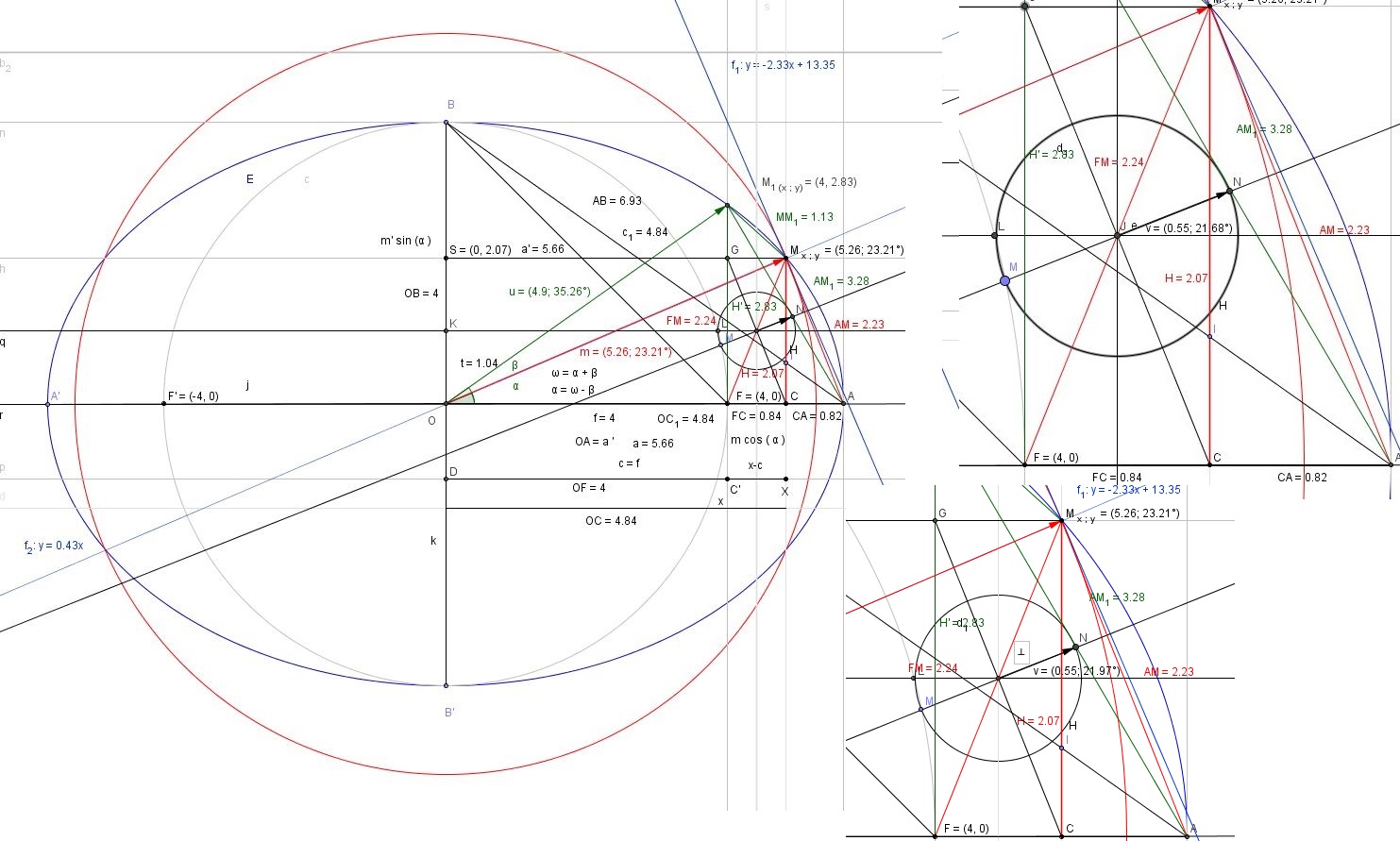
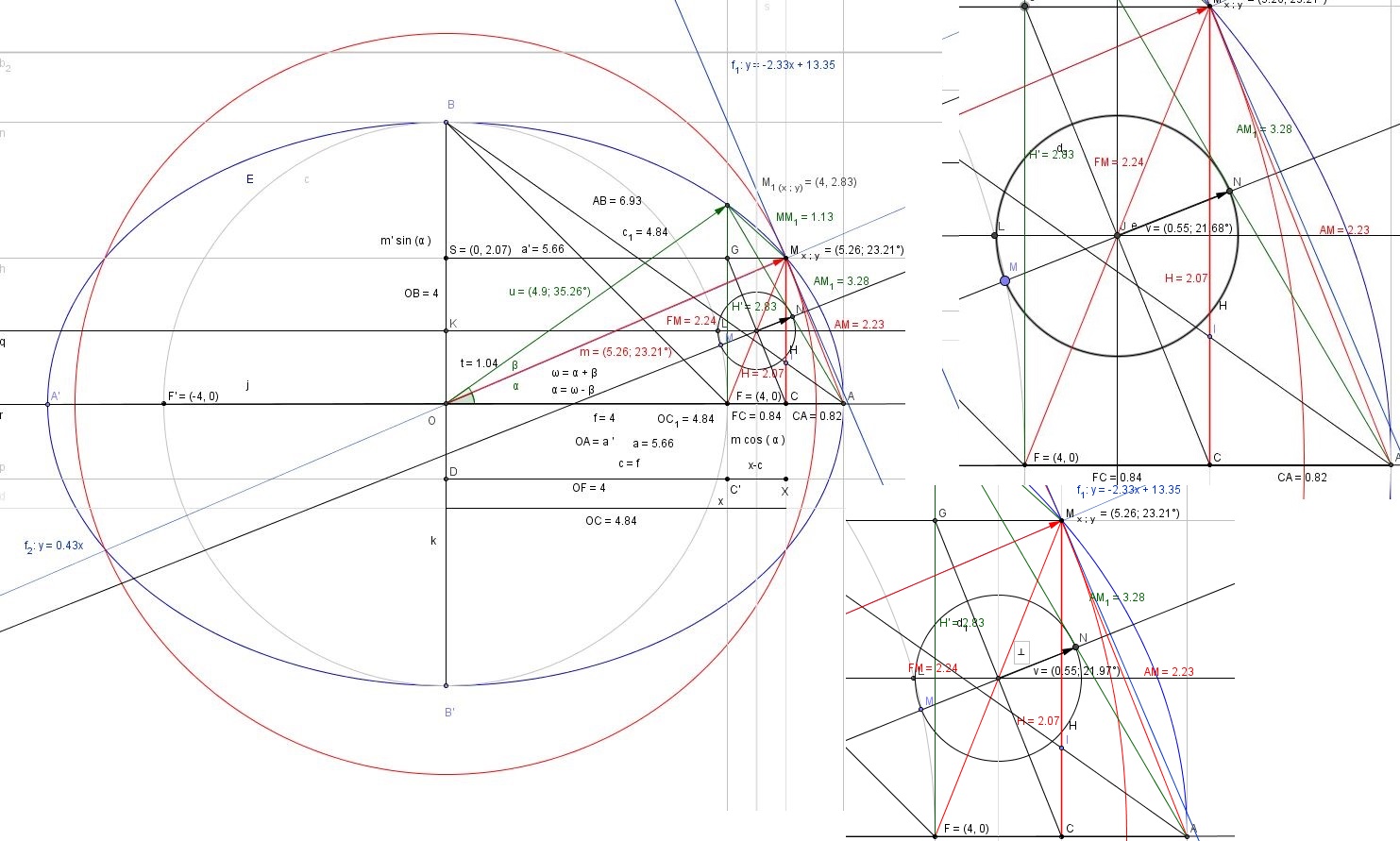
Toute la problématique est dans ce déssin, comment déterminer le vecteur OM, et par conséquent sa distance :
08 01 2016 - 8H57, Bien avec le théorème de Pythagore, j'obtiendrai les distance OF qui est donnée, FM_1 qui est son orthogonale et donc OM, de surcroit à l'aide des rapport trigonométrique, qui vont peut être me donner le rapport d'excentricité. Ensuite, j'ai la distance OA, OF, et donc AF, je n'ai pas l'angle alpha, mais peut être qu'avec le triangle d'al kaschi après quelques simplification ou rapport proportionnel, je pourrais peut être obtenir le rapport OM, Ensuite son projeté orthogonal pourra peut être calculer à l'aide du thérorème de Pythagore, ect. Bref, rien n'est sûr, mais peut être que je vais finir par déterminer les relations qui permettront d'obtenir OM, et FM
Par rapport à ce dessin :
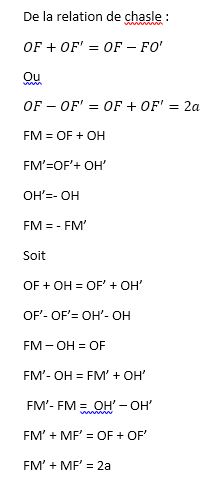
09-01-2016 : Bon, enfin une explication à ces formule :
http://www.mathcurve.com/courbes2d/engrenage/engrenage2.shtml
Tel qu'avant de réfléchir, j'allais établir le rapport suivant :
06 01 2015 - 05 H 59 :
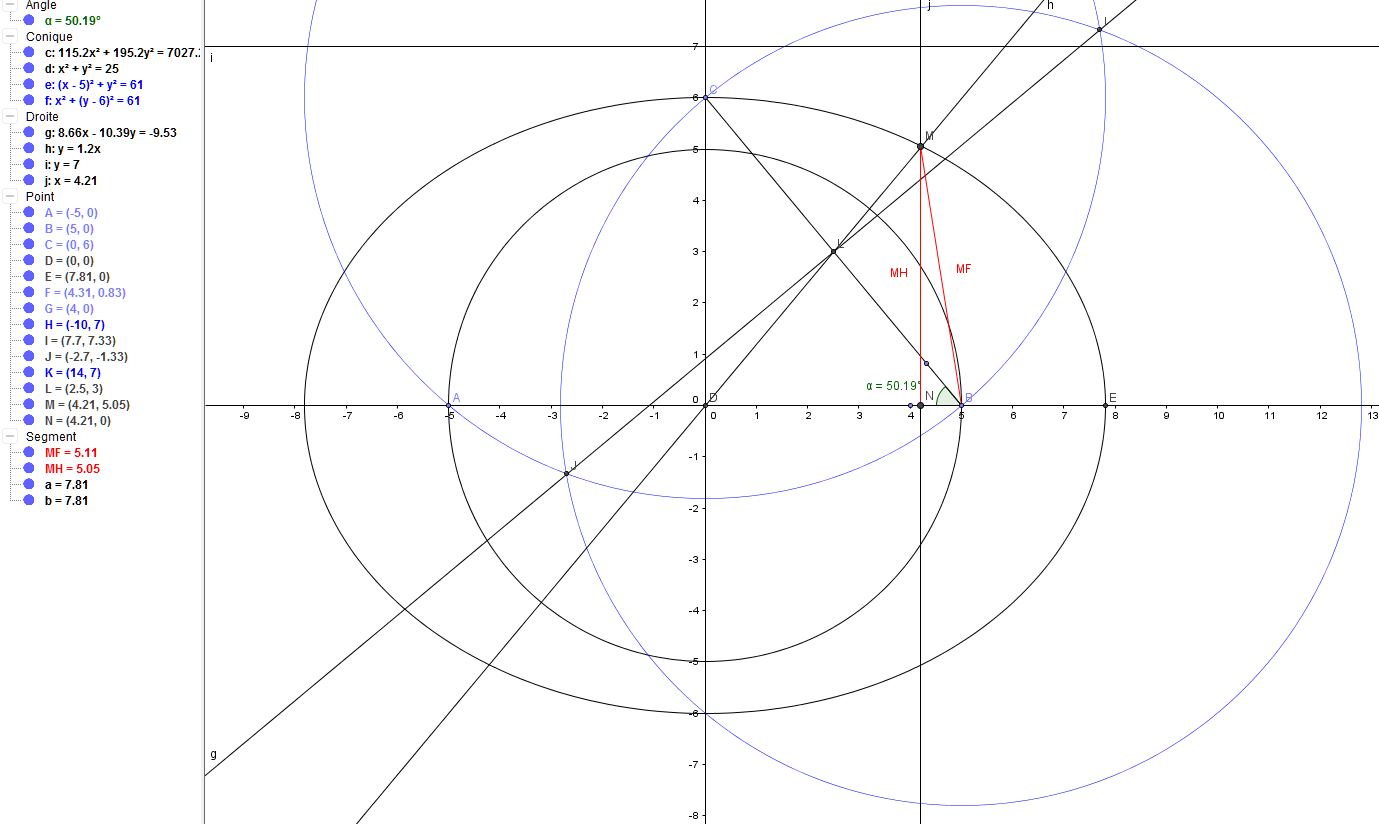
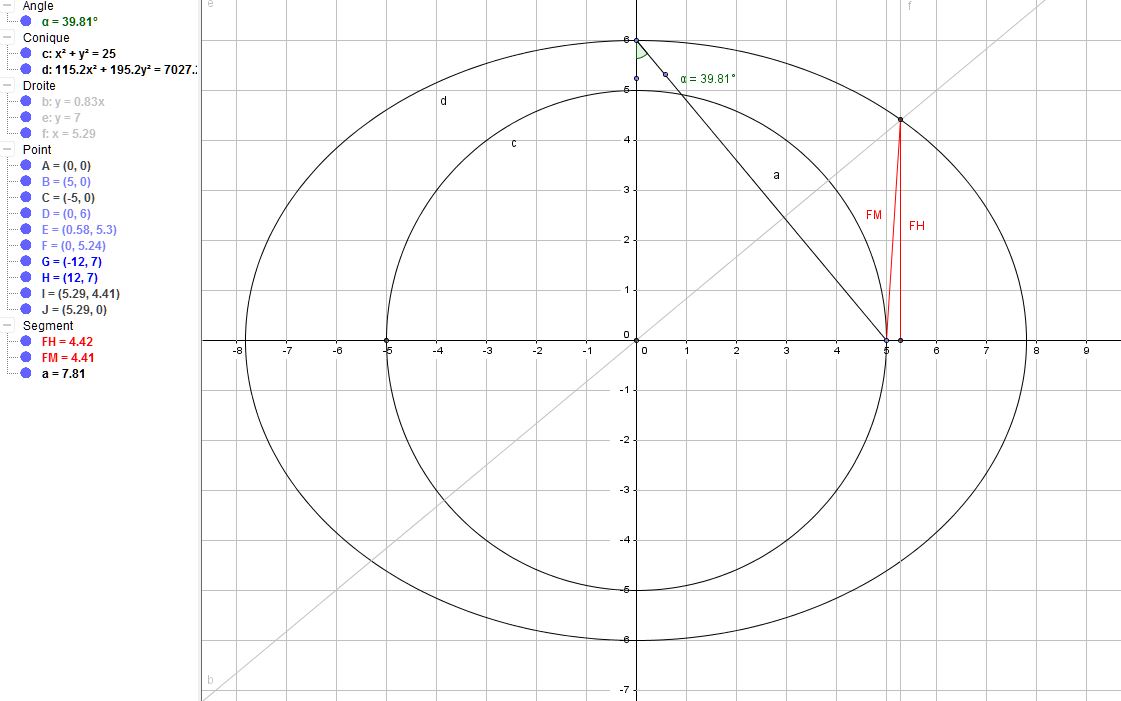
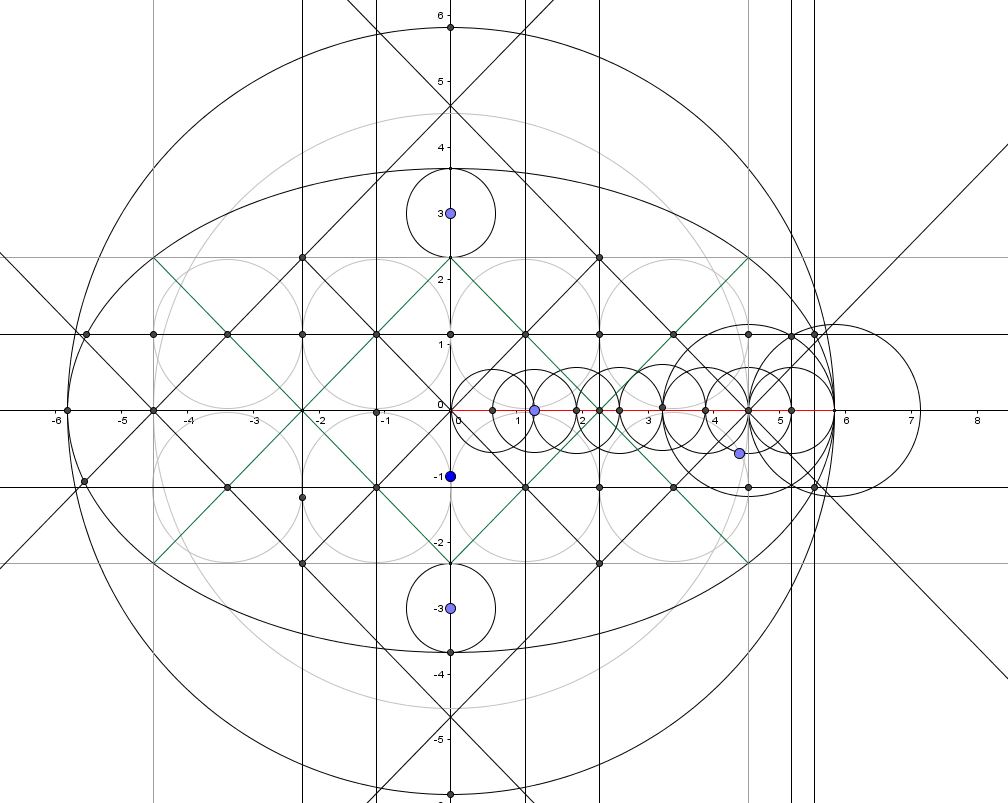
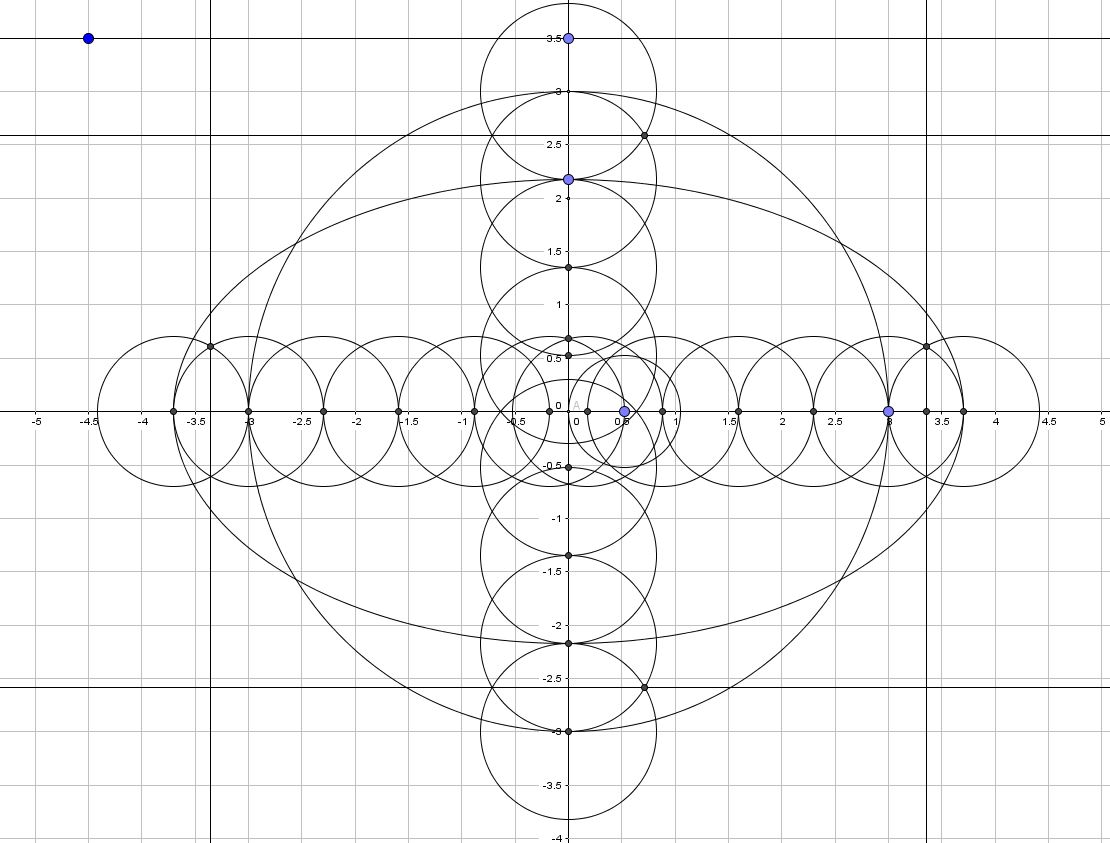
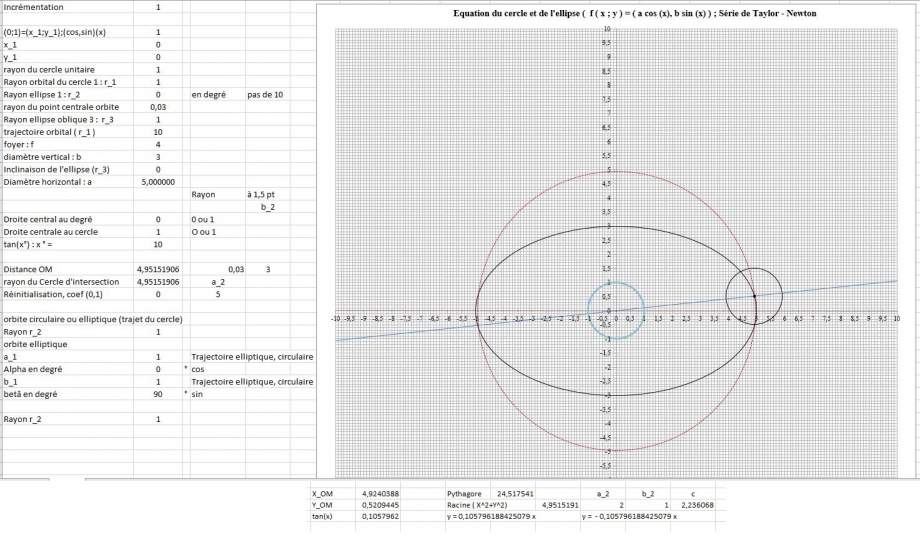
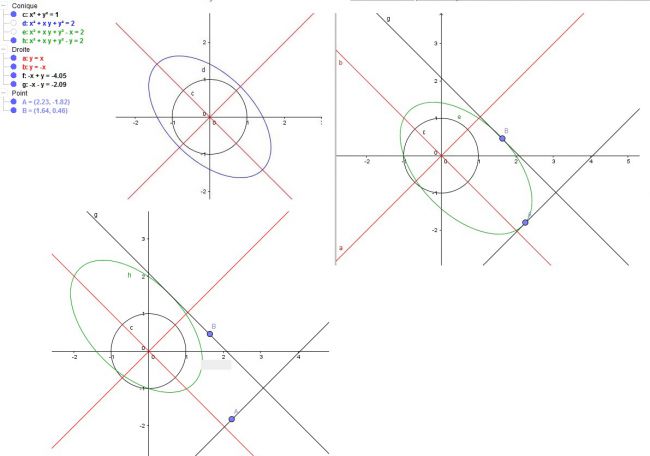
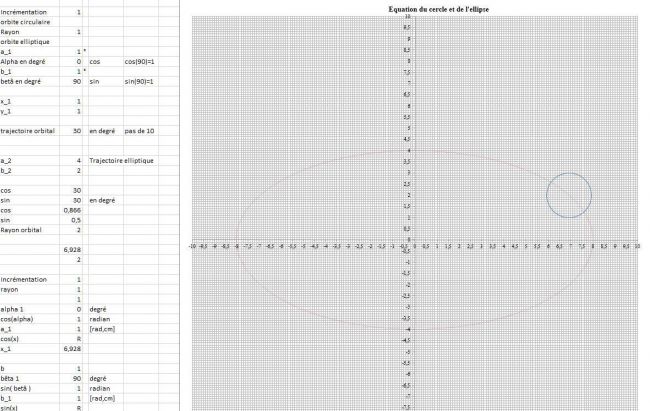
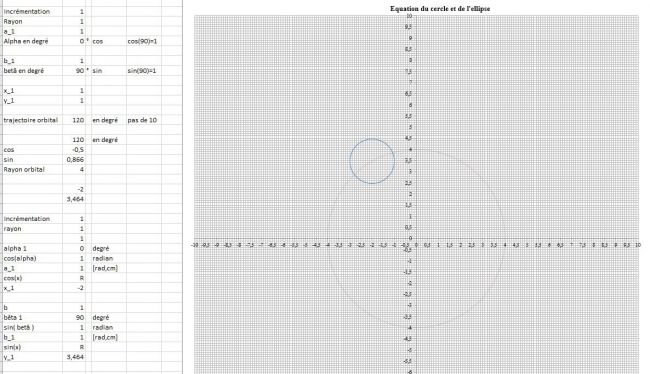
Intersection du cercle, de la droite et de l'ellipse
05 01 2015 - 14 H26 :
03 01 2015 06H10 :
Domach, deux élipse, deux séries numérique différentes. Celle de Newton, et la leur ou peut être la même avec des calculs différents. puisque les deux ellipse se ressemble. Ou peut être un coefficient qui permet d'elargir ou de réduire son élargissement.
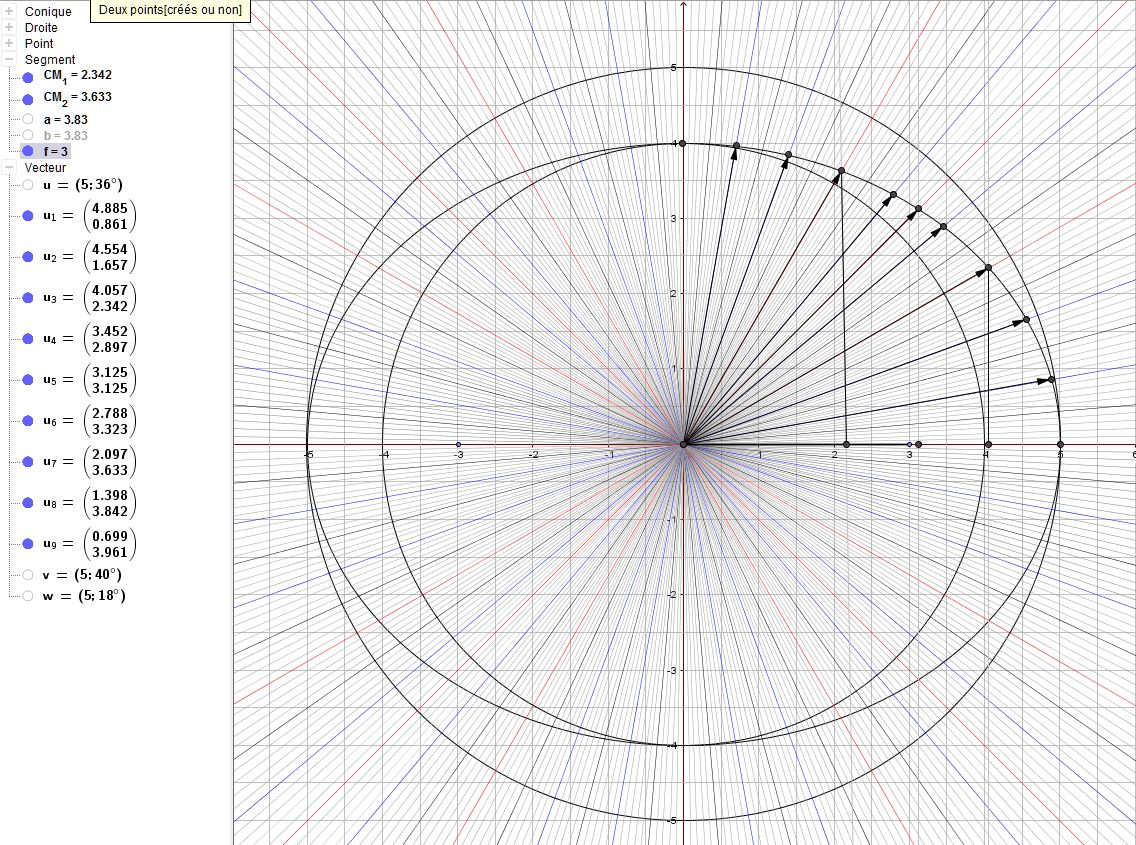
22H00 :
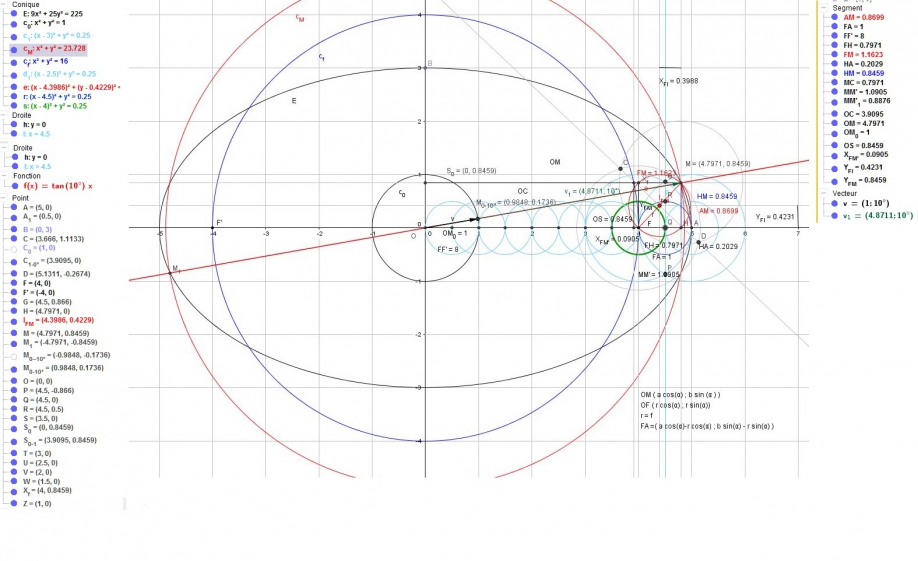
Tan(60°) x :
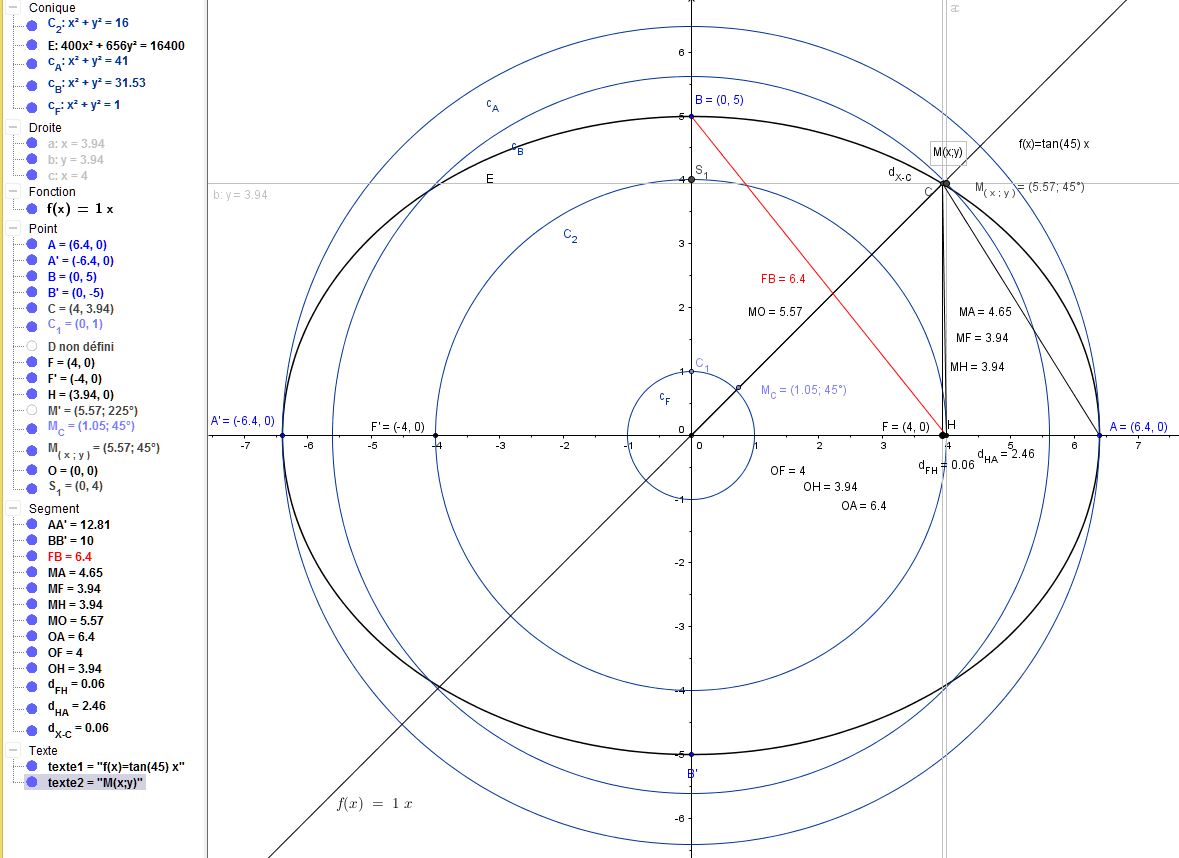
Tan(45°) x
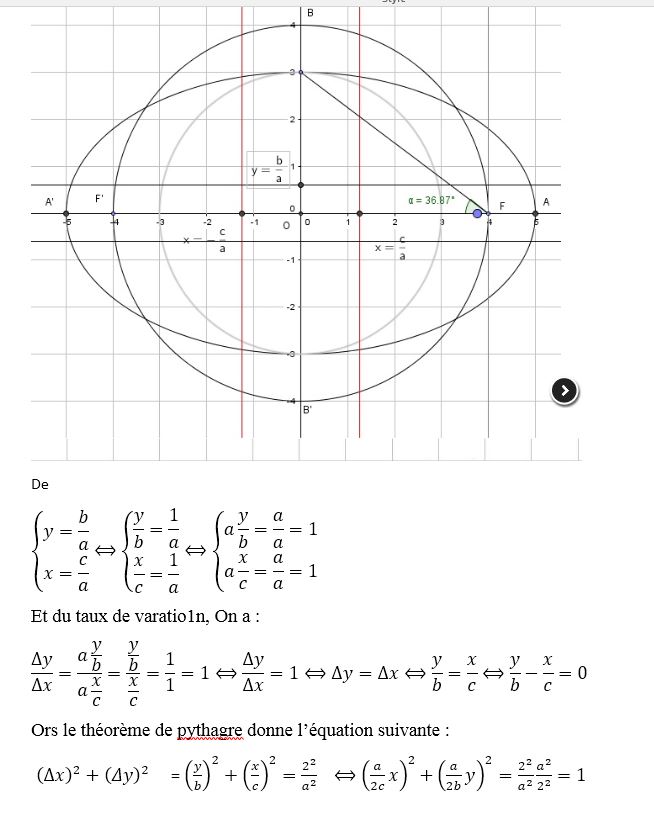
Bon, comme dans le formulaire, on constate qu'à 45° la distance entre le centre du rayon et le point du foyer est égal à la distance entre l'orthogonale projeté sur l'axe des absicsses et le rayon.
De plus, le rayon du cercle de la distances des ordonnées ou la distance OB tel que B est l'axe verticale de l'ellipse appelé petit axe
tan(30°) x :
03 01 2015 :
02-01-2016 - 03 H 40
02-01-2016 :
01-01-2016 ; 20H30-23H30
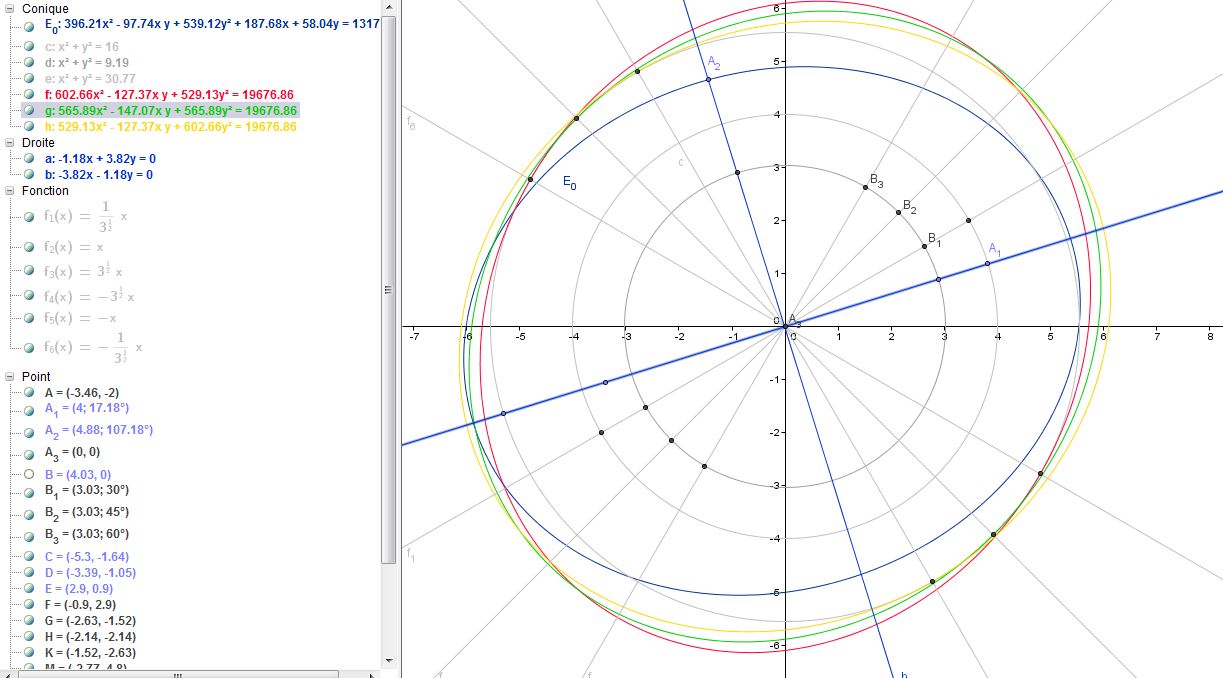
01 01 2016 15-16H : Rotation des ellipse par les symétrie orthogonale :
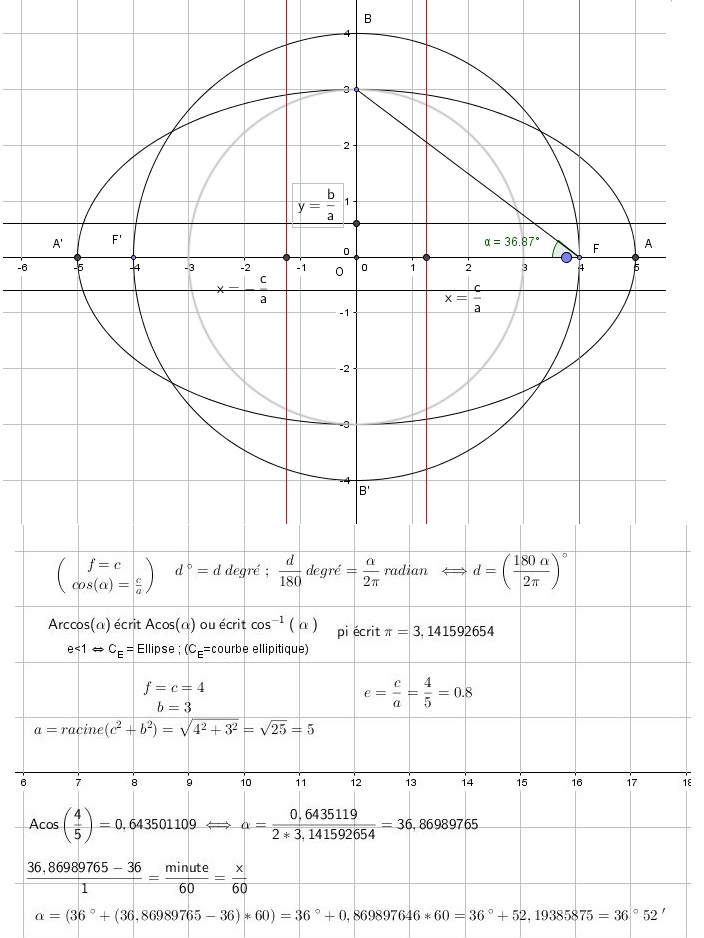
01 01 2016 14 h : Recherche des Foyer, directrice, excentricité
6h00 - 4h00
Mise en évidences des 1ère équations elliptique
4h00- 2h00
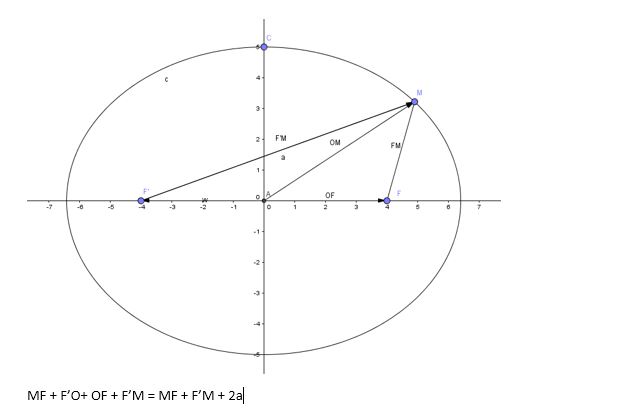
Bon, là ça ne m'étonne pas, et c'est évident cela prévisage rien de bon pour le coefficient d'excentricité e = c / a ou c / ka tel que MF + MF' = 2a
Décembre 2015, bon, en j'ai racheté en Novembre 2015, un ordinatateur. et Ms office, je l'ai depuis ce mois. mes dernière découverte sur ce sujet :
28-12-2015
29-12-2015
Mois de décembre avant le 22 - 12 2015 :
27 Janvier 2015 :
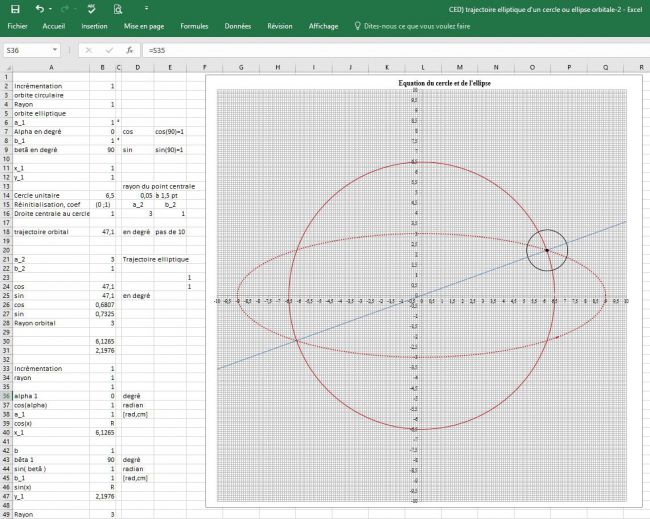
Bonjour, bon, suite à la découverte de l'ellipse (certes informatique), j'ai pu découvrir la sphère, ou le cercle elliptique qui donne un effet sphérique. bon, il est évident que je suis étonné que la formule de Taylor donne à la fois le cercle, l'ellipse et la sphère. Ceci dit, dans ma découverte, je peut déplacer l'ellipse à effet sphérique en coordonnées rectangulaire, grâce à x0 et y0, mais je pourrais aussi donner une nouvelle trajectoire elliptique avec un cercle invisible plus élévé permettant de créer une trajectoire elliptique en dehors de la sphère, et pour une planète, en dehors de sa stratosphère, ensuite à la place de x0, et y0, il suffit d'utiliser a r_2 sin (x) , b r_2 cos (x), pour pouvoir faire circuler une mini sphère sur l'éllipse 2 qui est en dehors de la sphère, ou du cerle munie d'une ellipse à l'interieur du cercle
________________________________________________________________________________________
Documentaire spatiaux :
Inscrivez-vous au blog
Soyez prévenu par email des prochaines mises à jour
Rejoignez les 26 autres membres