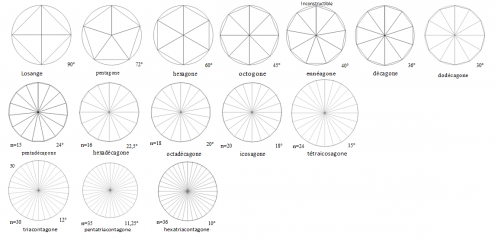
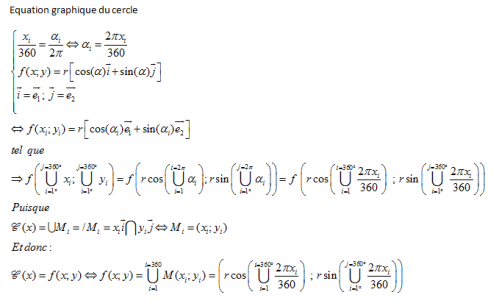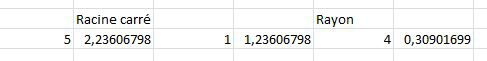GC) Polygone régulier isogonal
Géométrie
https://mathris.blog4ever.com/blog/articles-cat-310546-712505-geometries.html
_______________________________________________________________________________________________________________________
______________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________
Vidéo méthaphorique
l'Ennéagone (Inconstructible, Approximation)
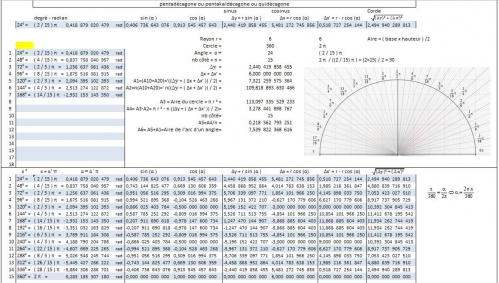
Le pentadécagone ;
Construction du Cercle et Ellipse
__________________________________________________________________________________________________________________________________
11 Novembre ; Ca va, c'est assez haut pour toi (bon, c'est pas wikipédia, mais calculatrice et tous les degré, ainsi que ses 0,5 degré)
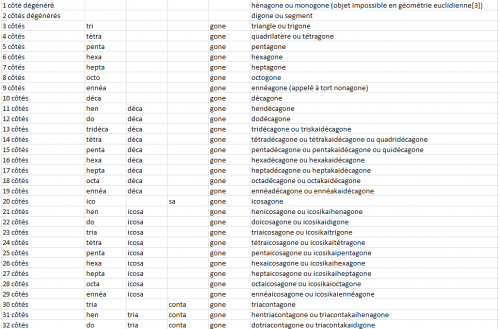
De wikipdia, nom des polygones,
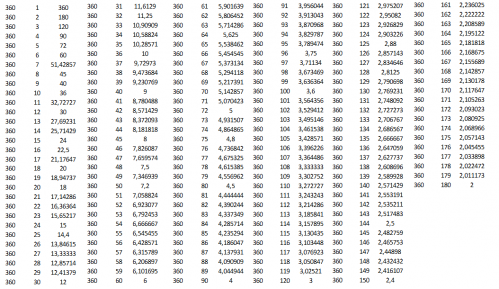
Polygone régulier de l'ensemble des nombres entiers N dans l'ensemble des nombre décimaux Z, ou ensemble des nombres rationnels (fraction) Q :
nb cercle côté degré nb cercle côté degré
| 1 | 360 | 1 | 360 | 21 | 360 | 16 | 22,5 | |
| 2 | 360 | 2 | 180 | 22 | 360 | 25 | 14,4 | |
| 3 | 360 | 3 | 120 | 23 | 360 | 32 | 11,25 | |
| 4 | 360 | 4 | 90 | 24 | 360 | 48 | 7,5 | |
| 5 | 360 | 5 | 72 | 25 | 360 | 50 | 7,2 | |
| 6 | 360 | 6 | 60 | 26 | 360 | 64 | 5,625 | |
| 7 | 360 | 8 | 45 | 27 | 360 | 75 | 4,8 | |
| 8 | 360 | 9 | 40 | 28 | 360 | 80 | 4,5 | |
| 9 | 360 | 10 | 36 | 29 | 360 | 96 | 3,75 | |
| 10 | 360 | 12 | 30 | 30 | 360 | 100 | 3,6 | |
| 11 | 360 | 15 | 24 | 31 | 360 | 125 | 2,88 | |
| 12 | 360 | 18 | 20 | 32 | 360 | 128 | 2,813 | |
| 13 | 360 | 20 | 18 | |||||
| 14 | 360 | 24 | 15 | |||||
| 15 | 360 | 30 | 12 | |||||
| 16 | 360 | 36 | 10 | |||||
| 17 | 360 | 40 | 9 | |||||
| 18 | 360 | 16 | 22,5 | |||||
| 19 | 360 | 45 | 8 | |||||
| 20 | 360 | 120 | 3 |
Bon, voilà, la liste est très limité en nombre de polygones régulier
__________________________________________________________________________________________________________________________________
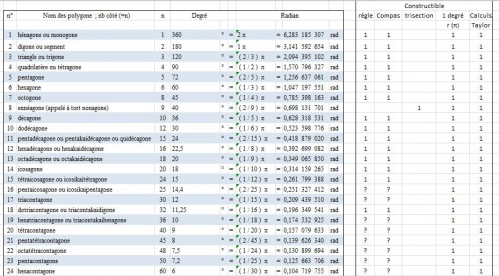
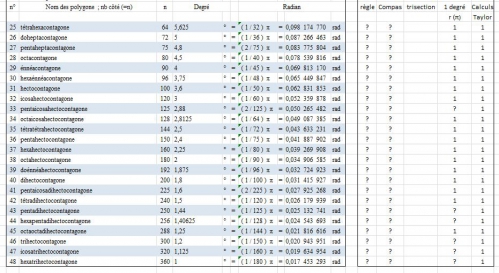
Nom des polygones réguliers (wikipédia) , Mes calculs informatiques (pgcd et ppcm * 1000) :
| n° | Nom des polygone ; nb côté (=n) | n | Degré | Radian | |||||
| 1 | hénagone ou monogone | 1 | 360 | ° | = | 2 π | = | 6,283 185 307 | rad |
| 2 | digone ou segment | 2 | 180 | ° | = | 1 π | = | 3,141 592 654 | rad |
| 3 | triangle ou trigone | 3 | 120 | ° | = | ( 2 / 3 ) π | = | 2,094 395 102 | rad |
| 4 | quadrilatère ou tétragone | 4 | 90 | ° | = | ( 1 / 2 ) π | = | 1,570 796 327 | rad |
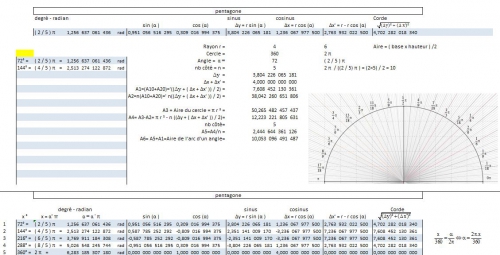
| 5 | pentagone | 5 | 72 | ° | = | ( 2 / 5 ) π | = | 1,256 637 061 | rad |
| 6 | hexagone | 6 | 60 | ° | = | ( 1 / 3 ) π | = | 1,047 197 551 | rad |
| 7 | octogone | 8 | 45 | ° | = | ( 1 / 4 ) π | = | 0,785 398 163 | rad |
| 8 | ennéagone (appelé à tort nonagone) | 9 | 40 | ° | = | ( 2 / 9 ) π | = | 0,698 131 701 | rad |
| 9 | décagone | 10 | 36 | ° | = | ( 1 / 5 ) π | = | 0,628 318 531 | rad |
| 10 | dodécagone | 12 | 30 | ° | = | ( 1 / 6 ) π | = | 0,523 598 776 | rad |
| 11 | pentadécagone ou pentakaidécagone ou quidécagone | 15 | 24 | ° | = | ( 2 / 15 ) π | = | 0,418 879 020 | rad |
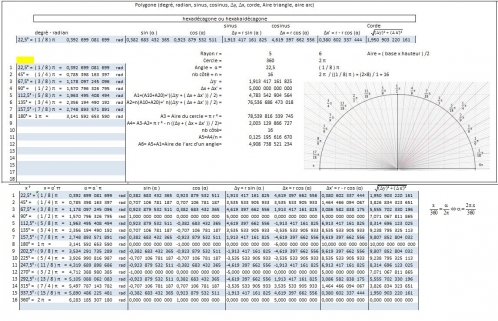
| 12 | hexadécagone ou hexakaidécagone | 16 | 22,5 | ° | = | ( 1 / 8 ) π | = | 0,392 699 082 | rad |
| 13 | octadécagone ou octakaidécagone | 18 | 20 | ° | = | ( 1 / 9 ) π | = | 0,349 065 850 | rad |
| 14 | icosagone | 20 | 18 | ° | = | ( 1 / 10 ) π | = | 0,314 159 265 | rad |
| 15 | tétraicosagone ou icosikaitétragone | 24 | 15 | ° | = | ( 1 / 12 ) π | = | 0,261 799 388 | rad |
| 16 | pentaicosagone ou icosikaipentagone | 25 | 14,4 | ° | = | ( 2 / 25 ) π | = | 0,251 327 412 | rad |
| 17 | triacontagone | 30 | 12 | ° | = | ( 1 / 15 ) π | = | 0,209 439 510 | rad |
| 18 | dotriacontagone ou triacontakaidigone | 32 | 11,25 | ° | = | ( 1 / 16 ) π | = | 0,196 349 541 | rad |
| 19 | hexatriacontagone ou triacontakaihexagone | 36 | 10 | ° | = | ( 1 / 18 ) π | = | 0,174 532 925 | rad |
| 20 | tétracontagone | 40 | 9 | ° | = | ( 1 / 20 ) π | = | 0,157 079 633 | rad |
| 21 | pentatétracontagone | 45 | 8 | ° | = | ( 2 / 45 ) π | = | 0,139 626 340 | rad |
| 22 | octatétracontagone | 48 | 7,5 | ° | = | ( 1 / 24 ) π | = | 0,130 899 694 | rad |
| 23 | pentacontagone | 50 | 7,2 | ° | = | ( 1 / 25 ) π | = | 0,125 663 706 | rad |
| 24 | hexacontagone | 60 | 6 | ° | = | ( 1 / 30 ) π | = | 0,104 719 755 | rad |
| 25 | tétrahexacontagone | 64 | 5,625 | ° | = | ( 1 / 32 ) π | = | 0,098 174 770 | rad |
| 26 | doheptacontagone | 72 | 5 | ° | = | ( 1 / 36 ) π | = | 0,087 266 463 | rad |
| 27 | pentaheptacontagone | 75 | 4,8 | ° | = | ( 2 / 75 ) π | = | 0,083 775 804 | rad |
| 28 | octacontagone | 80 | 4,5 | ° | = | ( 1 / 40 ) π | = | 0,078 539 816 | rad |
| 29 | énnéacontagone | 90 | 4 | ° | = | ( 1 / 45 ) π | = | 0,069 813 170 | rad |
| 30 | hexaénnéacontagone | 96 | 3,75 | ° | = | ( 1 / 48 ) π | = | 0,065 449 847 | rad |
| 31 | hectocontagone | 100 | 3,6 | ° | = | ( 1 / 50 ) π | = | 0,062 831 853 | rad |
| 32 | icosahectocontagone | 120 | 3 | ° | = | ( 1 / 60 ) π | = | 0,052 359 878 | rad |
| 33 | pentaicosahectocontagone | 125 | 2,88 | ° | = | ( 2 / 125 ) π | = | 0,050 265 482 | rad |
| 34 | octaicosahectocontagone | 128 | 2,8125 | ° | = | ( 1 / 64 ) π | = | 0,049 087 385 | rad |
| 35 | tétratétrahectocontagone | 144 | 2,5 | ° | = | ( 1 / 72 ) π | = | 0,043 633 231 | rad |
| 36 | pentahectocontagone | 150 | 2,4 | ° | = | ( 1 / 75 ) π | = | 0,041 887 902 | rad |
| 37 | hexahectocontagone | 160 | 2,25 | ° | = | ( 1 / 80 ) π | = | 0,039 269 908 | rad |
| 38 | octahectocontagone | 180 | 2 | ° | = | ( 1 / 90 ) π | = | 0,034 906 585 | rad |
| 39 | doénnéahectocontagone | 192 | 1,875 | ° | = | ( 1 / 96 ) π | = | 0,032 724 923 | rad |
| 40 | dihectocontagone | 200 | 1,8 | ° | = | ( 1 / 100 ) π | = | 0,031 415 927 | rad |
| 41 | pentaicosadihectocontagone | 225 | 1,6 | ° | = | ( 2 / 225 ) π | = | 0,027 925 268 | rad |
| 42 | tétradihectocontagone | 240 | 1,5 | ° | = | ( 1 / 120 ) π | = | 0,026 179 939 | rad |
| 43 | pentadihectocontagone | 250 | 1,44 | ° | = | ( 1 / 125 ) π | = | 0,025 132 741 | rad |
| 44 | hexapenditahectocontagone | 256 | 1,40625 | ° | = | ( 1 / 128 ) π | = | 0,024 543 693 | rad |
| 45 | octaoctadihectocontagone | 288 | 1,25 | ° | = | ( 1 / 144 ) π | = | 0,021 816 616 | rad |
| 46 | trihectocontagone | 300 | 1,2 | ° | = | ( 1 / 150 ) π | = | 0,020 943 951 | rad |
| 47 | icosatrihectocontagone | 320 | 1,125 | ° | = | ( 1 / 160 ) π | = | 0,019 634 954 | rad |
| 48 | hexatrihectocontagone | 360 | 1 | ° | = | ( 1 / 180 ) π | = | 0,017 453 293 | rad |
Polygone constructible :
____________________________________________________________________________
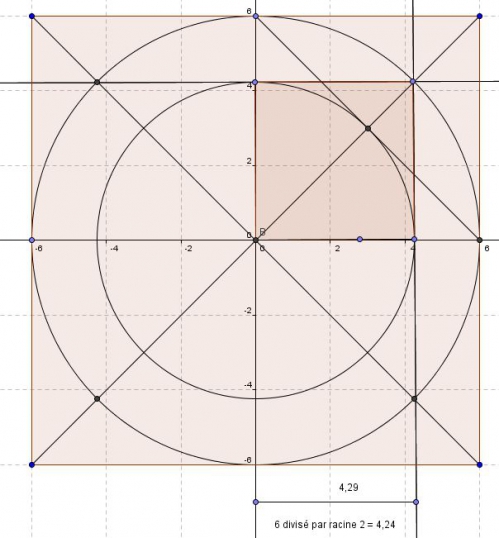
Les Polygones réguliers : (Posséder chez soi Géogébra, et Java plug in) :
Bon, vu que j'ai enregistrer de chez moi, n'oublier pas d'activer dans votre géogébra votre navigation de construction par étape
Remarque 1 :
Oh merde le millénium, j'ai véritablement la science infuse, incroyable ? ? ? :
Angle-d'or-de-Fabionnacci--Construction-et-Formule-numérique-feuille-dynamique.html
Construction d'une maison, (1984-1986), Ennéagone
Pentagone_d'or de Fabonnacci modifié.html
Le 23 Octobre 2014
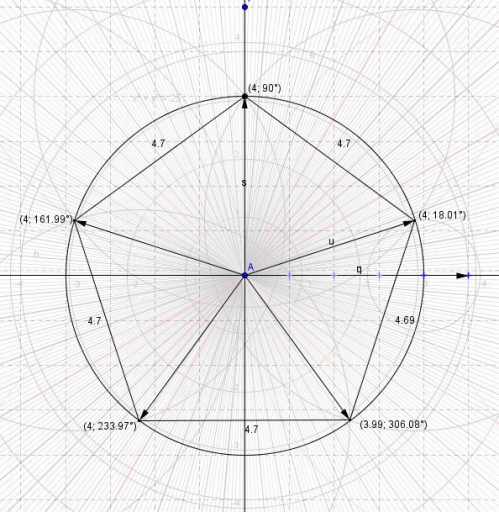
Le pentagone avec le degré ( bon, c'est la copie, et donc, il manque quelque 0,01 à 0,03 degré. Ceci dit sans dimension, nous avons à la règle les dimensions équidistantes.
Autre construction de pentagone :
Pentagone__intersection_de_cercles_.html
Pentagone, intersection de cercles _36°__18°_.html
Le degré régulier ( division d'arc par 2)
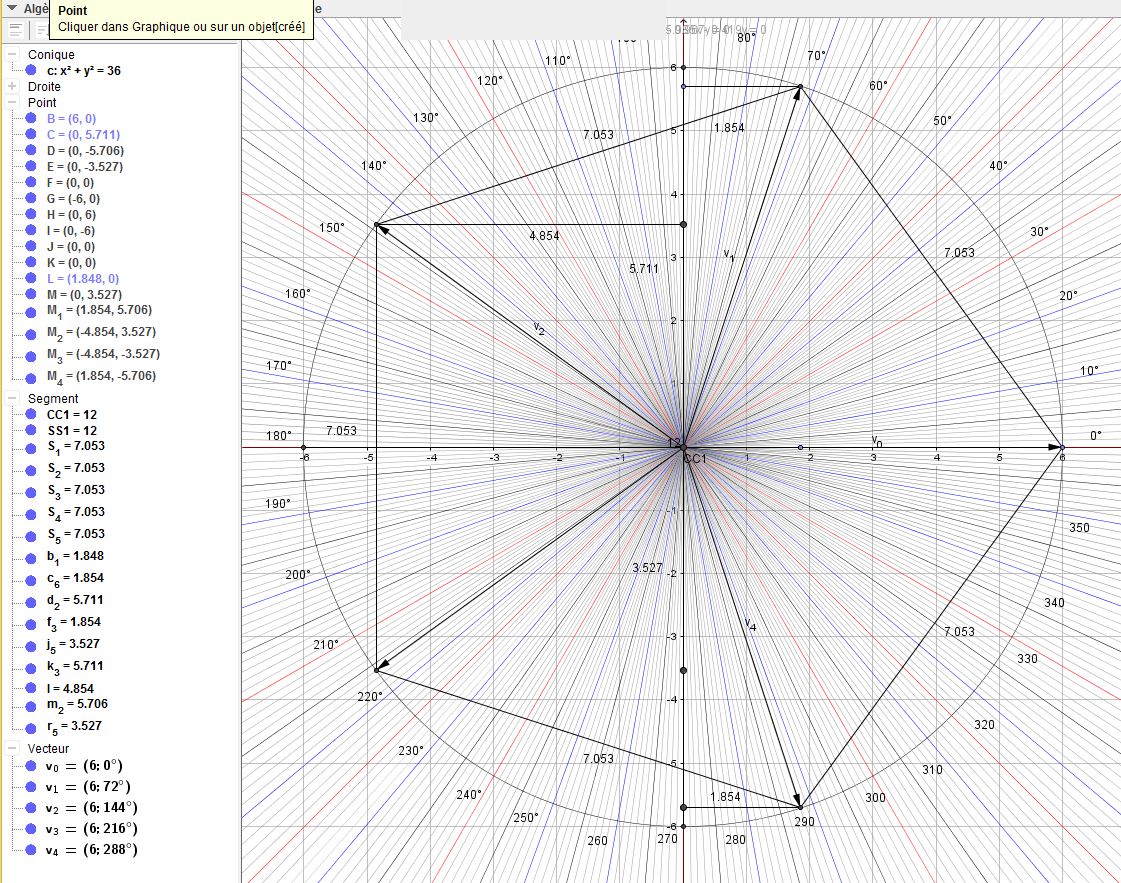
Pentagone radial ou polaire par le Degré de Taylor - Fibonacci
__________________________________________________________________________________________________________________________________
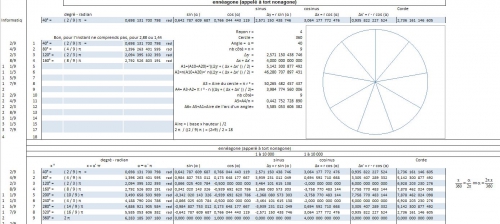
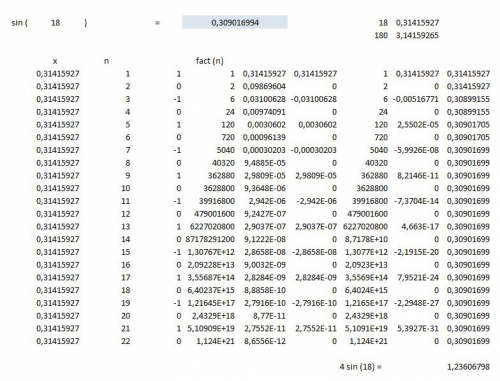
Nonagone ou Ennéagone, 18 degré.html
Bon comme Gauss, l'énnéagone est une figure inconnstructible à la règle et au compas. toutefois, on peut obtenir une bonne approximation, soit atteindre 319,94 à 319,99
Méthode 1 : Calcul par les dérivées de Newton et la formule de Taylor
Extrait ( je suis en train de les ranger par groupe, long, et fastidieux ). Soit c'est vraiment le vrai raporteur officiel, cette fois, sans l'ombre d'un doute :
Construction du 01 degré officiel
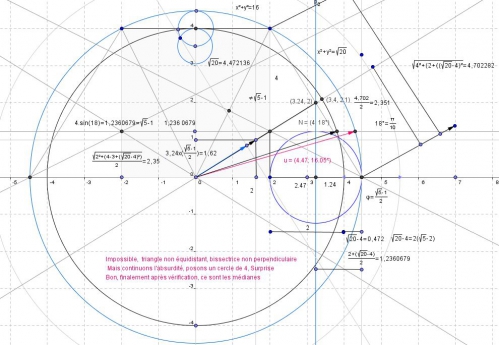
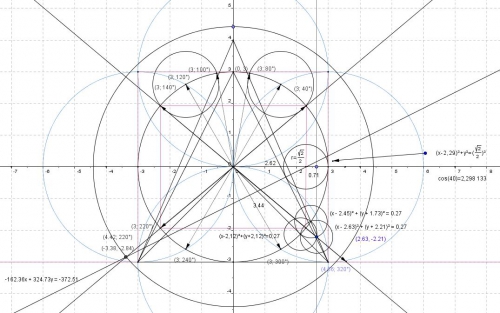
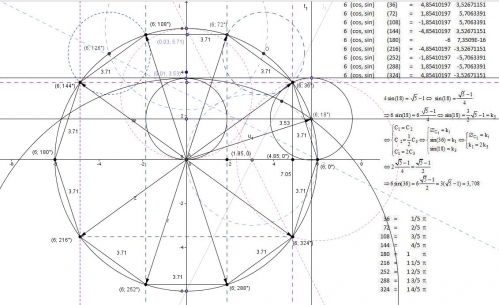
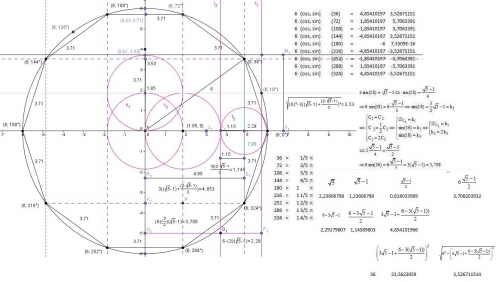
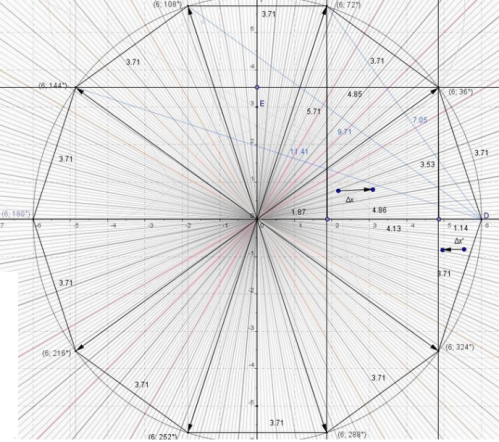
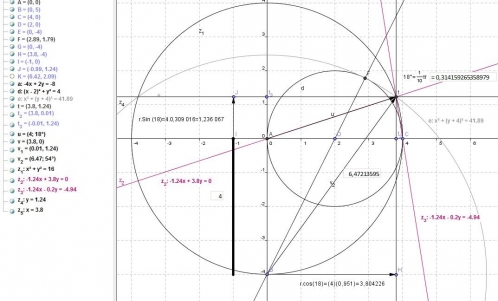
Méthode 2 : par la recherche d'une symétrie :
Polygone__angle_44_01__36_degr--__40_degr--_stricte_.html
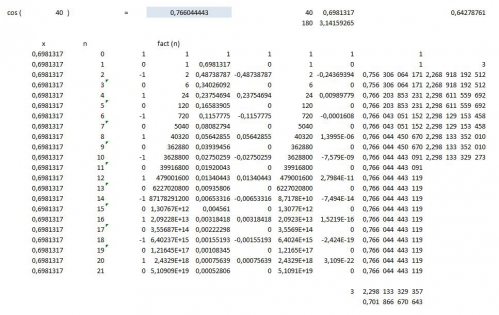
3 cos(
Dans ce dessin, j'ai cru tenir enfin la loi, en réalité, nous avons dans (0,5)², soit racine carré de 2 sur 2, en fait 3- 3 cos (40) = 0,701 866. alros que racine carré ( 2 ) / 2 = 0,707 062 Soit seul les séries de Taylor permettent d'obtenir en informatique à 10^-3, la valeur 40 degré de manière surement très précise, de là à dire que cos (40) est une valeur exacte, elle est déjà une valeur approximative.
12/11/2014 : Bon, j'ai refait ce soir, j'ai trouvé un résultat différent soit 44,5. bon, je me suis trompé, puisqu'au maximum, j'aurais du obtenir:
| 36 | + | 44,04 -36 | = | 36 4,02 | = | 40,02 |
| ──────── | ||||||
| 2 |
Pour toute explication diverse et complète voir journal mathématique/géométrie polygonale :
https://mathris.blog4ever.com/geometrie-polygonale
__________________________________________________________________________________________________________________________________
Documentation
La trisection des angles (Gauss, Wantzel ... ) :
http://debart.pagesperso-orange.fr/histoire/trisection_angle.html
http://www.les-mathematiques.net/phorum/read.php?8,435086,436149
Trisection de l'angle de 40 degré ( ? ) :
http://www.chateau-de-mezerville.org/curiosites-geometriques/trace-enneagone.php
__________________________________________________________________________________________________________________________________
Tracé circulaire de l'énnéagone :
http://fr.wikipedia.org/w/index.php?title=Enn%C3%A9agone
__________________________________________________________________________________________________________________________________
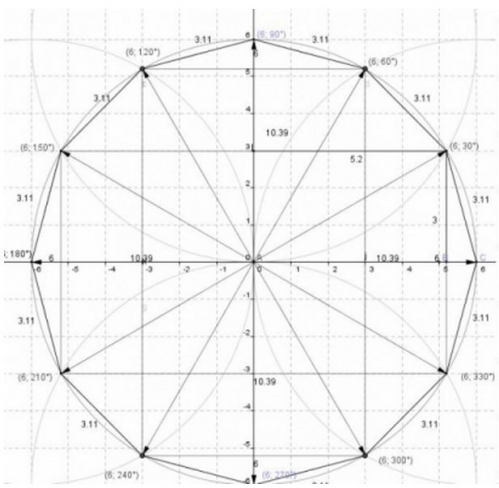
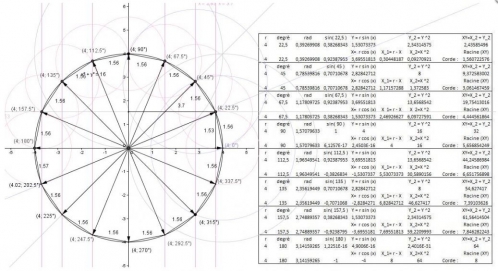
Décagone, intercercle, symétrie, Cordes.html
Le 27 Octobre 2014
Décagone4 - Intercercles, Symétries, Cordes, Coordonées, Valeur numerique.html
Alors, afin d'éviter les 0,1 ou 0,01, ou 0,2, j'ai utiliser les cercles et les symétries orthogonales projeté sur l'axe des cosinus et par extension des abscisses, bon comme je le constate, la 108 n'est pas tout à fait 108 degré, mais inversement la 208 degré est elle strictement, qui est la droite oblique formant l'angle 108 degré.
De plus la particularité de ce degré que je sois à 36,02 ou non, conserve bien la distance equidistante du décagone, formant un polygone régulier stricte, ce qui est l'essentiel du polygone.
Bon, voilà, c'est le degré le plus précis au monde entre 1 à 3 10^-2 près à intervalle régulier de sûr, puisque c'est le même cercle au minimètre. Il n'y a pas mieux, et il n'y aura pas mieux, Seul le théorème de Pythagore en calcul automatique pourra faire mieux, mais avec des intervals inégaux. Et c'est dit.
Construction par la tengante de la symétrie, (attention, 23,51, 23,91, 23,99
Construction de l'angle 24 degré :
Pentad--cagone__24_degr--__figure_1.html
_Pentad--cagone__figure_2__24_degr--.html
Construction du pentadécagone
Calcul des cordes :
Pentad--cagone01_36_60_24_degr--.html
Construction du pentadécagone à partir du rapporteur :
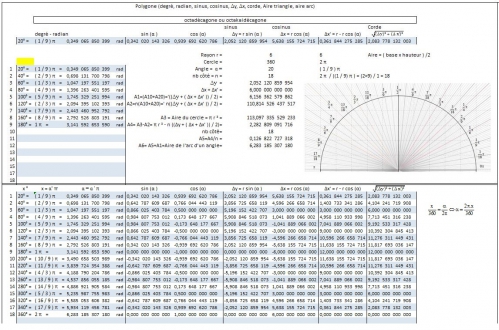
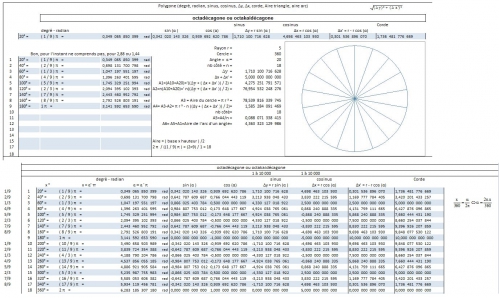
Polygone__20_degré, Octadécagone-.html
Isocontagone_avec_rapporteur_03.html
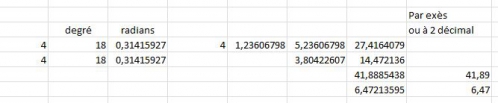
Bon, je ne me suis pas fatigué, calculé sur excel, l'un sur 180, l'autre sur 180, soit à vérifié après 180 tel que pi (1/8) pi = ( 9 / 8) pi
Au cas où les images ne serait pas aussi net ( Effet Zoom et de pagination) :
2015 : Bon, avec l'ancienne version, mon degré, même à l'écran correspond au rapporteur. Il est évident qu'il faut le refaire ou réactualiser à chaque version de Windows (et peut d'écran ?) , Cette fois, vous allez pouvoir vous amuser réellement avec les vraies grandeurs, bonne chance, c'est du boulot, avec une variante, cette fois (à cause de la redondance, du temps, j'utilse la méthode de Newton - Taylor pour la 40 degré, et la symétrie de Fibonnacci, ce qui m'a souris), En plus si vous voulez le faire, cela va vite ( 2h - 4h) :
Cercle de 360 degré par les formules de Newton - Taylor
2013 - 2014 :
Le degré :
Pour l'instant Album photo , page 3,5 et 4 :
- Décagone1.pdf
- Construction du degré polygonale
-
Recherche Recherche du degré numérique
Le degré (feuille dynamique de géogébra) :
rapporteur___1____0_087266_01_.html
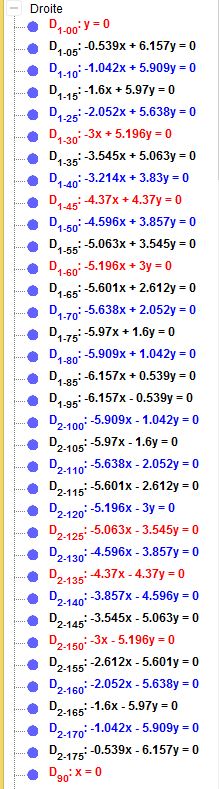
Vérification des angles :
rapporteur__degré par la droite__.html
Image :
____________________________________________________
Rectificatif le 20 Novembre 2014, influant sur la corde (avec toutes mes excuse :
Calcul-de-la-corde-23-11-2014--21h24.xlsx
06 Décembre 2014 (apparement, cette fois réglé, mais sait on jamais, n'efface pas la version précédente pour l'instant) :
Calcul-de-la-corde-06-12-2014--10h46.xlsx
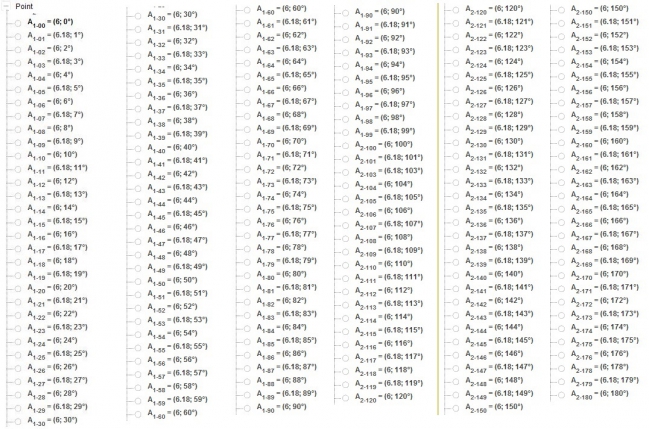
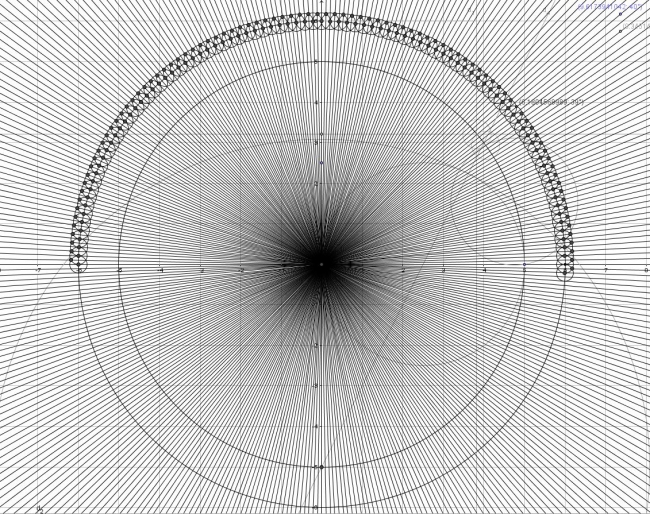
Rapporteur ( (sans les rosaces) ; (Attention la copie 2,3,....n de la copie 1, 2, ....... faussera les rapports de plus en plus) ) :
rapporteur___1____0_087266_01____Copie.html
____________________________________________________
Bon c'est à refaire, mais en attendant, vous avez toutes les angles en radian et en fraction
23-11-2014 :
21 h :
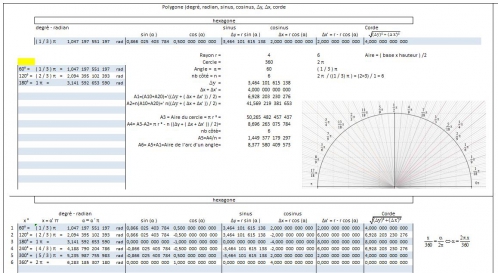
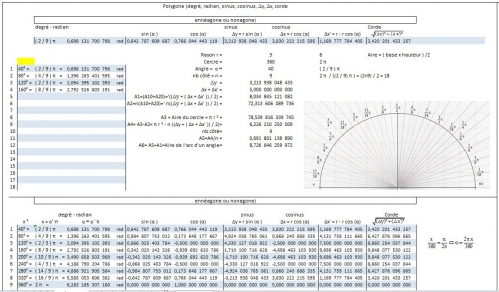
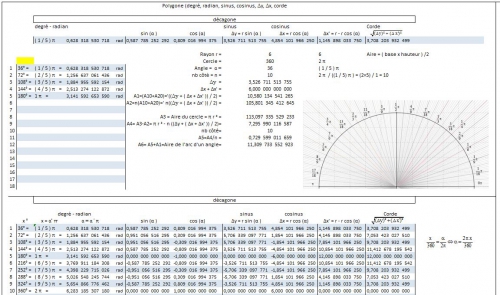
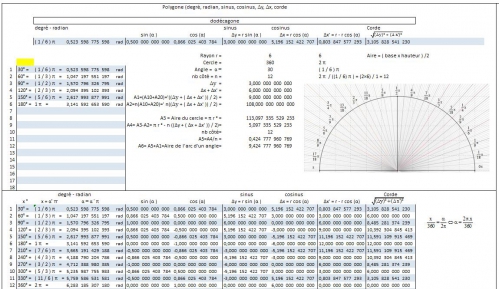
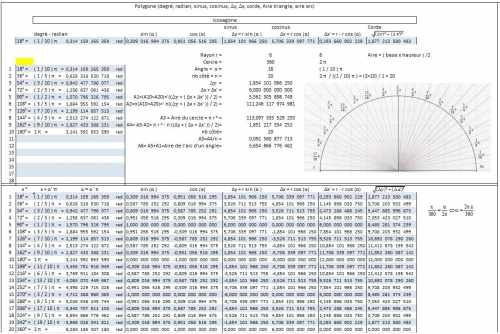
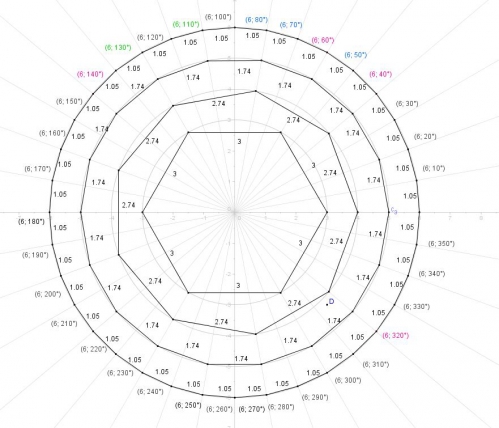
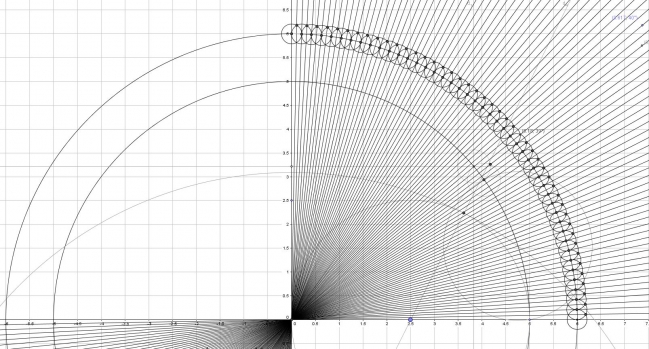
Bon, la télé au foot en parlait (Chaine ). Je vous ai rajouté des déssins excel proportionnel, mais non dimensionnel. Comme ça si vous voulez rajouter le dessins avec le calculs d'angle, des cordes, et d'aire, vous pourrez les rajouter. Vous pouvez aussi faire vous même les programmes, et prendre les déssins ou les changer de couleur. En tout les cordes sont faites au moins.
10 h - 16h
hier, j'étais fatigué, soit j'en avais un peu marre, je ne fais pas atttention, mais les polygone régulier à nombre entier, n'était pas afficher, là, idem, je n'ai pas envie de me crever le cul pour l'instant, donc j'ai rajouté un contrôle pour pouvoir afficher les nombres entier. Bon, l'image, ce n'est pas un polygone, mais le fromage, ce qui est une excellente représentation. Quand à celui qui veut son vrai polygone, il n'a plus qu'à relier les fils, et photographier.
23-11-2014 - 0H50
Toujours pas résolu, mais à modifier la mise en forme, soit quand l'angle est faux, il n'est pas afficher, c'est une amélioration.
22-11-2014
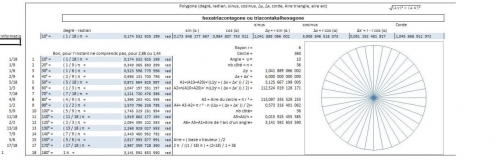
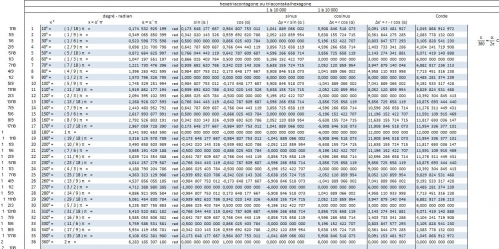
Bon, là ce sont les polygones fractionnaire, soit des polygones régulier avec un segment décimal de dimension finie qui déconnent, et hormis d'éxecuter manuellement une puissance de 10, je ne peux pas faire grand chose.
17-11-2014
degré-1-degré à 5-cm--différence et division des cordes.docx
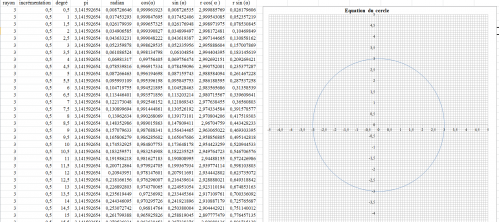
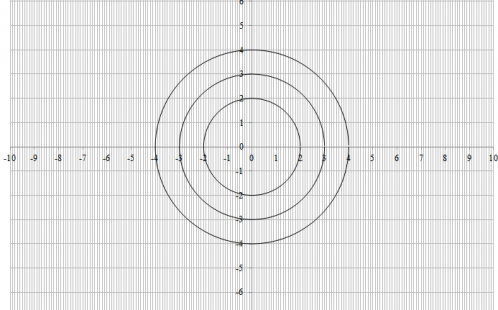
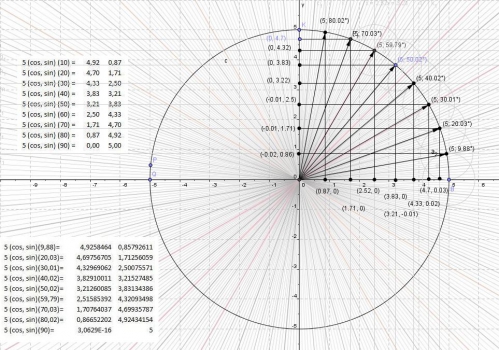
Représentation graphique de l'Equation du Cercle :
Ecriture de l'équation du cercle graphique :
Graphe-de-l'équation-du-cercle.xlsx
Et donc de l'ellipse, de l'hyperbole puisque racine carré de (a b).
______________________________________________________________________________________________________________________________________________
_____________________________________________________________________________________________
Compléments : historique logique du nombre d'or avant le fameux nombre d'or
Pour la petite histoire (n'a pas envie de copier, ni travailler pour l'instant ) :
Origine du nombre d'or ? :
Préparation des théories alpha numérique :
Bon, on y pense pas forcément, mais ce logiciel en sachant que les chiffres sont des calculs numérique par pythagore et non pas des prises de mesures, est complétement hallucinant, Soit de moi même, j'ai tout de même une mesure inconnue que je ne peux pas calculer formellement à cause des décimal. Malheureusement s'il utilise les mêmes méthodes que moi, nous n'aurions pas les intersections de cercles, soit les vraies valeurs numérique et donc trigonométrique qui est soit celle affiché, soit complétement virtuel.
C'est surement l'une formules :
m ( x- a) ( X - X0) ( Y -Y0 ) sin ( v ) = r ²
ρ ( x -a ) cos ( α ) ( y -b) sin ( α )
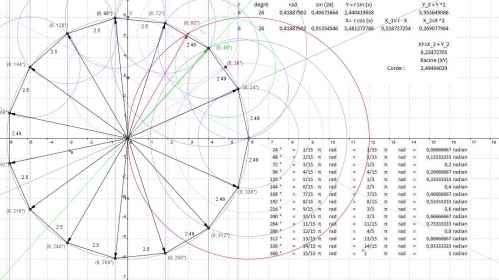
Valeur numérique du nombre d'or de Fabonnacci :
On rappelle que cosinus et sinus sont une suite de valeurs numérique représentant somme des dérivées premières, seconde, tiers, .... nième :
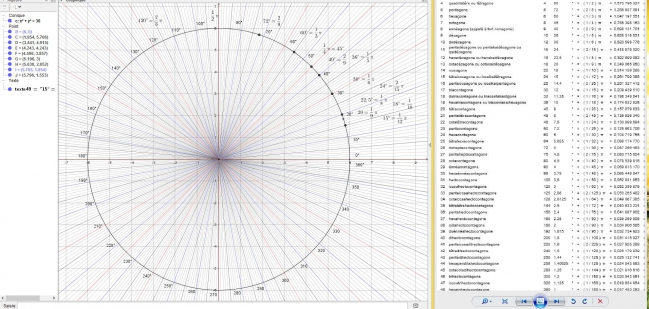
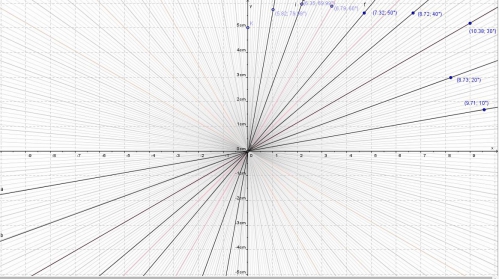
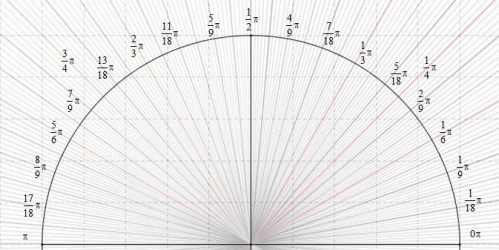
Cette image est encore moins utilisable sur géogébra, elle est grossit à 120 % pour obtenir un ordre de grandeur en radian (World - Math type) :
Copie de la copie du degré sur géogébra, inutilisable dans géogébra
____________________________________________________________________________________________
____________________________________________________________________________________________
Cercle divisé en 360 parties :
http://www.concept-global.net/mathematiques/lien_geometrique_cercle_systeme_sexagesimal_gif.htm
http://fr.wikipedia.org/wiki/Sp%C3%A9cial:Recherche/Degr%C3%A9_(angle
https://mathris.blog4ever.com/blog/photos-310546-3.html
___________________________________________________________________________
Liens web :
Science Ch : http://www.sciences.ch/htmlfr/geometrie/geometrieformes01.php
Pentagone : http://ww3.ac-poitiers.fr/math/prof/resso/ima/bay2/index.htm
Nombre et curiosité : http://villemin.gerard.free.fr/Construc/Dodecago.htm
Création Mandala : http://www.lame-agit.fr/polygonesetoiles.html
Math curve : http://www.mathcurve.com/polyedres/regulier/polygoneregulier.shtml
Wikipédia : http://fr.wikipedia.org/wiki/Polygone
Math et tiques : http://ymonka.free.fr/maths-et-tiques/index.php/detentes/noms-des-polygones
Apple Works : http://document.pagesperso-orange.fr/polygones.htm
Math World
http://mathworld.wolfram.com/search/?query=polygonal&x=0&y=0
http://mathworld.wolfram.com/RegularPolygon.html
Indépendant, freelance :
http://abdelhafidmohad.free.fr/fichierpdf/Polygones.pdf
_____________________________________________________________________________________________
Axe trigonométrique, corde, Aire :
http://calculis.net/aire/segment-disque
http://fr.wikipedia.org/wiki/Cercle
_________________________________________________________________________
Retour sur rubrique
Géométrie classique
https://mathris.blog4ever.com/blog/articles-cat-310546-537596-geometrie_classique.html
___________________________________________________________________________
Géoméries
https://mathris.blog4ever.com/blog/articles-cat-310546-712505-geometries.html
_____________________________________________________________________________________________
Crée le 05 03 2014
A découvrir aussi
Inscrivez-vous au blog
Soyez prévenu par email des prochaines mises à jour
Rejoignez les 26 autres membres